Diện tích hình phẳng giới hạn bởi các đường thẳng y = - x , n ế u x ≤ 1 x - 2 , n ế u x > 1 và y = 10 3 x - x 2 là a/b . Khi đó a + 2b bằng
A. 16
B. 15
C. 17
D. 18
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\left(x+1\right)e^x=0\Rightarrow x=-1\)
\(S=\int\limits^0_{-2}\left|\left(x+1\right)e^x\right|dx=-\int\limits^{-1}_{-2}\left(x+1\right)e^xdx+\int\limits^0_{-1}\left(x+1\right)e^xdx\)
\(=\dfrac{2e-2}{e^2}\)

Chọn B.
Phương trình hoành độ giao điểm của hai đồ thị hàm số y = x3 + 3x và y = -x là: x3 + 4x = 0 ⇔ x = 0
Ta có: x3 + 4x ≤ 0, ∀ x ∈ [-2;0].
Do đó:
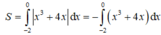
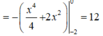

Phương trình hoành độ giao điểm:
\(x^2+1=x+3\Leftrightarrow x^2-x-2=0\Rightarrow\left[{}\begin{matrix}x=-1\\x=2\end{matrix}\right.\)
\(S=\int\limits^2_{-1}\left|x^2-x-2\right|dx=\int\limits^2_{-1}\left(-x^2+x+2\right)dx=\left(-\dfrac{1}{3}x^3+\dfrac{1}{2}x^2+2x\right)|^2_{-1}=\dfrac{9}{2}\)
Chọn C.
Ta có 10 3 x - x 2 = - x ⇒ x = 0 10 3 x - x 2 = x - 2 ⇒ x = 3
Suy ra a=13 ; b=2 và a+2b=17.