Tìm tổng các giá trị của m để hai phương trình z 2 + mz + 2 = 0 và - z 2 + 2z + m có ít nhất một nghiệm phức chung.
A. -2
B. 3
C. 1
D. 5
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Giả sử hai phương trình đã cho có nghiệm phức chung z 0 khi đó ta có hệ phương trình:
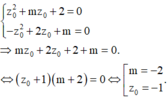
TH1: Nếu m = -2 thì khi đó 2 phương trình trở thành: z 2 − 2 z + 2 = 0 trùng nhau nên có nghiệm chung.
TH2: Nếu z 0 = − 1 thay vào hệ ta được:
1 − m + 2 = 0 − 1 − 2 + m = 0 ⇔ m = 3 .
Vậy giá trị cần tìm là m = -2 và m = 3.


2.giải phương trình trên , ta được :
\(x_1=\frac{-m+\sqrt{m^2+4}}{2};x_2=\frac{-m-\sqrt{m^2+4}}{2}\)
Ta thấy x1 > x2 nên cần tìm m để x1 \(\ge\)2
Ta có : \(\frac{-m+\sqrt{m^2+4}}{2}\ge2\) \(\Leftrightarrow\sqrt{m^2+4}\ge m+4\)( 1 )
Nếu \(m\le-4\)thì ( 1 ) có VT > 0, VP < 0 nên ( 1 ) đúng
Nếu m > -4 thì ( 1 ) \(\Leftrightarrow m^2+4\ge m^2+8m+16\Leftrightarrow m\le\frac{-3}{2}\)
Ta được : \(-4< m\le\frac{-3}{2}\)
Tóm lại, giá trị phải tìm của m là \(m\le\frac{-3}{2}\)

Bài 1 : a, Thay m = -2 vào phương trình ta được :
\(x^2+8x+4+6+5=0\Leftrightarrow x^2+8x+15=0\)
Ta có : \(\Delta=64-60=4>0\)
Vậy phương trình có 2 nghiệm phân biệt
\(x_1=\frac{-8-2}{2}=-5;x_2=\frac{-8+2}{2}=-3\)
b, Đặt \(f\left(x\right)=x^2-2\left(m-2\right)x+m^2-3m+5=0\)
\(f\left(-1\right)=\left(-1\right)^2-2\left(m-2\right)\left(-1\right)+m^2-3m+5=0\)
\(1+2\left(m-2\right)+m^2-3m+5=0\)
\(6+2m-4+m^2-3m=0\)
\(2-m+m^2=0\)( giải delta nhé )
\(\Delta=\left(-1\right)^2-4.2=1-8< 0\)
Vậy phương trình vô nghiệm
c, Để phương trình có nghiệm kép \(\Delta=0\)( tự giải :v )

\(z^2-2\left(2m-1\right)z+m^2=0\)
Theo Vi - ét, ta có :
\(\left\{{}\begin{matrix}z_1+z_2=-\dfrac{b}{a}=2\left(2m-1\right)=4m-2\\z_1z_2=\dfrac{c}{a}=m^2\end{matrix}\right.\)
Ta có :
\(z^2_1+z_2^2=2\)
\(\Leftrightarrow\left(z_1+z_2\right)^2-2z_1z_2=2\)
\(\Leftrightarrow\left(4m-2\right)^2-2m^2-2=0\)
\(\Leftrightarrow16m^2-16m+4-2m^2-2=0\)
\(\Leftrightarrow14m^2-16m+2=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}m=1\\m=\dfrac{1}{7}\end{matrix}\right.\)
Ta có phương trình bậc hai trên tập số phức:
z^2 - 2(2m-1)z + m^2 = 0
Theo định lý giá trị trung bình, nếu z1 và z2 là nghiệm của phương trình trên, thì ta có:
z1 + z2 = 2(2m-1) và z1z2 = m^2
Từ phương trình z1^2 + z2^2 = 2, ta suy ra:
(z1+z2)^2 - 2z1z2 = 4
Thay z1+z2 và z1z2 bằng các giá trị đã biết vào, ta được:
(2(2m-1))^2 - 2m^2 = 4
Đơn giản hóa biểu thức ta có:
m^2 - 4m + 1 = 0
Suy ra:
m = 2 + √3 hoặc m = 2 - √3
Vậy, để phương trình có hai nghiệm phân biệt thỏa mãn z1^2 + z2^2 = 2, ta cần phải có m = 2 + √3 hoặc m = 2 - √3.
Kết luận: Có hai giá trị của m để phương trình có hai nghiệm phân biệt thỏa mãn z1^2 + z2^2 = 2, đó là m = 2 + √3 hoặc m = 2 - √3.
Đáp án C
Giả sử hai phương trình đã cho có nghiệm phức chung z 0 khi đó ta có hệ phương trình:
TH1: Nếu m = -2 thì khi đó 2 phương trình trở thành: z 2 - 2z + 2 trùng nhau nên có nghiệm chung.
TH2: Nếu z 0 = -1 thay vào hệ ta được:
Vậy giá trị cần tìm là m = -2 và m = 3.