Phần tự luận
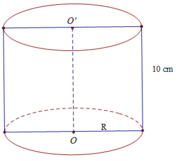
Cho hình trụ có đường sinh bằng 10 cm và diện tích xung quanh của hình trụ bằng 160π ( c m 2 ). Tính:
a) Diện tích toàn phần của hình trụ.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
4 tháng 11 2019
b) Thể tích hình trụ:
V = π R 2 h = π. 8 2 .10 = 640π ( c m 3 )
17 tháng 6 2021
Stp=2πrh+2πr2
=2πr.5+2πr2
=10πr+2πr2
Sxq=2πrh
=2πr.5
=10πr
Theo đề bài ta có Sxq=\(\dfrac{1}{2}\)Stp
<=>\(\dfrac{10\text{π}r+2\text{π}r^2}{2}=10\text{π}r\)
<=>\(20\text{π}r=10\text{π}r+2\text{π}r^2\)
<=>\(10\text{π}r=2\text{π}r^2\)
<=> r = 5 (cm)
AH
Akai Haruma
Giáo viên
27 tháng 6 2021
Lời giải:
Khái niệm đường sinh quen thuộc trong hình nón.
Như đề của bạn thì đường sinh chính là đường cao? Thế thì thể tích hình trụ: $\pi r^2h=\pi 3^2.2=18\pi$ (cm khối)
Nhưng mà diện tích xung quanh thì là: $2\pi rh=12\pi$ (cm vuông)
Thể tích và diện tích so sánh với nhau sao được?
a) Ta có:
Diện tích đáy: S đ á y = π R 2 = π. 8 2 = 64π ( c m 2 )
Diện tích toàn phần: S t p = S x q + 2 S đ á y = 160π + 2.64π = 288π ( c m 2 )