Có bao nhiêu giá trị nguyên của tham số mÎ[-10;10] để bất phương trình sau nghiệm đúng ∀ x ∈ R : 6 + 2 7 x + 2 - m 3 - 7 x - m + 1 2 x ≥ 0
A. 10
B. 9
C. 12
D. 11
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
17 tháng 2 2018
Đúng(0)
Những câu hỏi liên quan
CM
20 tháng 7 2019
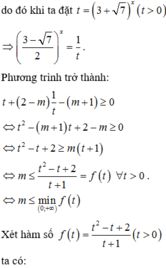
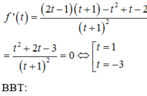
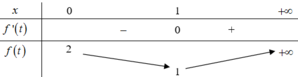
Chọn đáp án D
Phương pháp
Đồ thị hàm số y=f(x) và đường thẳng y=g(x) có duy nhất 1 điểm chung ⇒ phương trình hoành độ giao điểm f(x)=g(x) có nghiệm duy nhất.
Cách giải
Phương trình hoành độ giao điểm của đồ thị hai đồ thị hàm số là
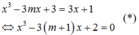
Hai đồ thị hàm số có duy nhất 1 điểm chung khi và chỉ khi phương trình (*) có nghiệm duy nhất
CM
9 tháng 9 2017
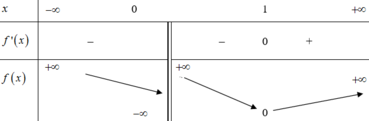
Nếu m = 0 thì phương trình trở thành 1 = 0 : vô nghiệm.
Khi m ≠ 0 , phương trình đã cho có nghiệm khi và chỉ khi
∆ = m 2 - 4 m ≥ 0 ⇔ m ≤ 0 m ≥ 4
Kết hợp điều kiện m ≠ 0 , ta được m < 0 m ≥ 4
Mà m ∈ Z và m ∈ [−10; 10] ⇒ m ∈ {−10; −9; −8;...; −1} ∪ {4; 5; 6;...; 10}.
Vậy có tất cả 17 giá trị nguyên m thỏa mãn bài toán.
Đáp án cần chọn là: A
CM
27 tháng 4 2018
Vậy có 8 giá trị nguyên của m thỏa mãn yêu cầu bài toán.
Đáp án D
CM
5 tháng 8 2017
Đáp án C
Đặt m + e x = a ; e x = b a ≥ 0 ; b > 0 ta có:
m + b = a m + a = b ⇔ m + b = a 2 m + a = b 2
⇔ m + b = a 2 b − a = a 2 − b 2 ⇔ m + b = a 2 a − b a + b + 1 = 0 ⇒ m = a 2 − b a = b
( Do a ≥ 0 ; b > 0 )
Khi đó m = b 2 − b b > 0
Do b 2 − b ≥ − 1 4 ∀ b > 0 nên phương trình có nghiệm khi m ≥ − 1 4
Do đó có 10 giá trị nguyên của m ∈ − 1 4 ; 10 thỏa mãn yêu cầu bài toán.