


Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




Đáp án C
Đặt t = 5 x t > 0
Khi đó PT ⇒ t 2 - m + 2 t + 2 m + 1 = 0 ⇔ t 2 - 2 t + 1 = m t - 2 *
Rõ ràng t = 2 không là nghiệm của phương trình
Do đó * ⇔ m = t 2 - 2 t + 1 t - 2 = t + 1 t - 2 = f t
Xét f(t) trên tập 0 ; 2 ∪ 2 ; + ∞ ta có: f ' t = 1 - 1 t - 2 2 = 0 ⇔ [ t = 1 t = 3
Mặt khác lim x → 0 f t = - 1 2 ; f 1 = 0 ; lim x → 2 - f t = - ∞ ; lim x → 2 + f t = + ∞ ; f 3 = 2 ; lim x → + ∞ f t = + ∞
Lập bảng biến thiên suy ra phương trình có nghiệm khi m ∈ ( - ∞ ; 0 ] ∪ [ 2 ; + ∞ )
Kết hợp m ∈ ℤ và m ∈ 0 ; 2018 suy ra có 2018 giá trị của tham số m.

Đáp án C
Đặt t = log 2 x với x ∈ 0 ; + ∞ thì t ∈ ℝ , khi đó bất phương trình trở thành t 2 + m t - m > 0 *
Để (*) nghiệm đúng với mọi t ∈ ℝ ⇔ ∆ * ≤ 0 ⇔ m 2 + 4 m ≤ 0 ⇔ m ∈ - 4 ; 0
Vậy có 5 giá trị nguyên của m thỏa mãn điều kiện

Đặt ![]()
Suy ra ![]()
Ta có ![]()
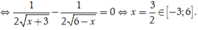
Ta có bảng biến thiên
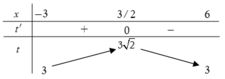
Từ bảng biến thiên ta suy ra ![]()
Khi đó bất phương trình trở thành: ![]()
![]()
Xét hàm số ![]() với
với ![]()
Ta có ![]()
Suy ra hàm số f(t) nghịch biến trên ![]()
![]()
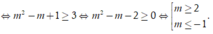
Chọn C.