Giải phương trình 1 + tan x = 2 2 sin x
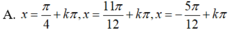
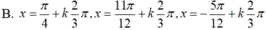
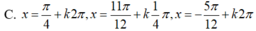
![]()
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




ĐKXĐ: \(x\ne\dfrac{k\pi}{2}\)
\(\dfrac{cosx}{sinx}-1=\dfrac{cos^2x-sin^2x}{1+\dfrac{sinx}{cosx}}+sin^2x-sinx.cosx\)
\(\Leftrightarrow\dfrac{cosx-sinx}{sinx}=cosx\left(cosx-sinx\right)-sinx\left(cosx-sinx\right)\)
\(\Leftrightarrow\left(cosx-sinx\right)\left(\dfrac{1}{sinx}-cosx+sinx\right)=0\)
\(\Leftrightarrow\left(cosx-sinx\right)\left(1-sinx.cosx+sin^2x\right)=0\)
\(\Leftrightarrow\left(cosx-sinx\right)\left(3-sin2x-cos2x\right)=0\)
\(\Leftrightarrow\left(cosx-sinx\right)\left(3-\sqrt{2}sin\left(2x+\dfrac{\pi}{4}\right)\right)=0\)

a.
\(\left(sin^2\dfrac{x}{2}+cos^2\dfrac{x}{2}\right)^2-2sin^2\dfrac{x}{2}cos^2\dfrac{x}{2}=\dfrac{1}{2}\)
\(\Leftrightarrow2-\left(2sin\dfrac{x}{2}cos\dfrac{x}{2}\right)^2=1\)
\(\Leftrightarrow1-sin^2x=0\)
\(\Leftrightarrow cos^2x=0\)
\(\Leftrightarrow x=\dfrac{\pi}{2}+k\pi\)
b.
\(\left(sin^2x+cos^2x\right)^3-3sin^2x.cos^2x\left(sin^2x+cos^2x\right)=\dfrac{7}{16}\)
\(\Leftrightarrow1-\dfrac{3}{4}\left(2sinx.cosx\right)^2=\dfrac{7}{16}\)
\(\Leftrightarrow16-12.sin^22x=7\)
\(\Leftrightarrow3-4sin^22x=0\)
\(\Leftrightarrow3-2\left(1-cos4x\right)=0\)
\(\Leftrightarrow cos4x=-\dfrac{1}{2}\)
\(\Leftrightarrow4x=\pm\dfrac{2\pi}{3}+k2\pi\)
\(\Leftrightarrow x=\pm\dfrac{\pi}{6}+\dfrac{k\pi}{2}\)



tham khảogiúp mình nhé: (tanx + cotx)^2 - (tanx + cotx) = 2? | Yahoo Hỏi & Đáp


a) \(\cos \left( {3x - \frac{\pi }{4}} \right) = - \frac{{\sqrt 2 }}{2}\;\;\;\; \Leftrightarrow \cos \left( {3x - \frac{\pi }{4}} \right) = \cos \frac{{3\pi }}{4}\;\;\; \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{3x - \frac{\pi }{4} = \frac{{3\pi }}{4} + k2\pi }\\{3x - \frac{\pi }{4} = - \frac{{3\pi }}{4} + k2\pi }\end{array}} \right.\;\;\;\; \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{3x = \pi + k2\pi }\\{3x = - \frac{\pi }{2} + k2\pi }\end{array}} \right.\)
\( \Leftrightarrow \;\left[ {\begin{array}{*{20}{c}}{x = \frac{\pi }{3} + \frac{{k2\pi }}{3}}\\{x = - \frac{\pi }{6} + \frac{{k2\pi }}{3}}\end{array}} \right.\;\;\left( {k \in \mathbb{Z}} \right)\)
b) \(2{\sin ^2}x - 1 + \cos 3x = 0\;\;\;\;\; \Leftrightarrow \cos 2x + \cos 3x = 0\;\; \Leftrightarrow 2\cos \frac{{5x}}{2}\cos \frac{x}{2} = 0\;\; \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{\cos \frac{{5x}}{2} = 0}\\{\cos \frac{x}{2} = 0}\end{array}} \right.\)
\( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{\frac{{5x}}{2} = \frac{\pi }{2} + k\pi }\\{\frac{{5x}}{2} = - \frac{\pi }{2} + k\pi }\\{\frac{x}{2} = \frac{\pi }{2} + k\pi }\\{\frac{x}{2} = - \frac{\pi }{2} + k\pi }\end{array}} \right.\;\;\;\;\;\;\; \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = \frac{\pi }{5} + \frac{{k2\pi }}{5}}\\{x = - \frac{\pi }{5} + \frac{{k2\pi }}{5}}\\{x = \pi + k2\pi }\\{x = - \pi + k2\pi }\end{array}} \right.\;\;\;\left( {k \in \mathbb{Z}} \right)\)
c) \(\tan \left( {2x + \frac{\pi }{5}} \right) = \tan \left( {x - \frac{\pi }{6}} \right)\;\; \Leftrightarrow 2x + \frac{\pi }{5} = x - \frac{\pi }{6} + k\pi \;\;\; \Leftrightarrow x = - \frac{{11\pi }}{{30}} + k\pi \;\;\left( {k \in \mathbb{Z}} \right)\)