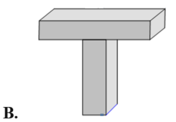
Giải thích tại sao hình 1.8c không phải là một khối đa diện?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
PT
1
Những câu hỏi liên quan
QT
Quoc Tran Anh Le
Giáo viên
16 tháng 12 2023
Ví dụ về vật không phải là vật rắn: quả bóng cao su, đệm, dây cung, ...
Tất cả những ví dụ trên đều không phải là vật rắn vì trong quá trình chuyển động thì vật bị biến dạng (khoảng cách giữa hai điểm bất kì thay đổi).
B
1
GN
GV Nguyễn Trần Thành Đạt
Giáo viên
1 tháng 2 2023
VD: quả bóng cao su
Vì những vật rắn khi chuyển động sẽ bị biến dạng mà tính đàn hồi của quả bóng cao su sẽ làm nó trở về trạng thái ban đầu ngay lập tức.
28 tháng 10 2023
- Nguyên tử khối của các nguyên tố hóa học không phải là các trị số nguyên vì các nguyên tố đều có ít nhất từ 2 đồng vị khác nhau và có số phần trăm số nguyên tử xác định.
- Đồng vị là những nguyên tử có cùng số đơn vị điện tích hạt nhân (cùng số proton) nhưng khác nhau số neutron. Nguyên tố hóa học là tập hợp các nguyên tử có cùng số đơn vị điện tích hạt nhân ⇒ Trong tự nhiên đã phát hiện được 94 nguyên tố.
CM
24 tháng 10 2019
Đáp án C.
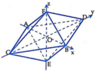
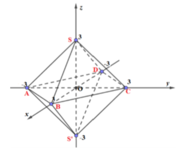
Ta có x + y + z = 3 ⇔ x 3 + y 3 + z 3 = 1 . Suy ra tập hợp các điểm M x ; y ; z là 8 mặt chắn có phương trình: ;
x 3 + y 3 + z 3 = 1 ; x − 1 + y − 3 + z − 3 = 1 ; x − 3 + y − 3 + z 3 = 1
x − 3 + y 3 + z − 3 = 1 ; x 3 + y − 3 + z − 3 = 1 ; x − 3 + y 3 + z 3 = 1 ; x 3 + y − 3 + z 3 = 1 ; x 3 + y 3 + z − 3 = 1
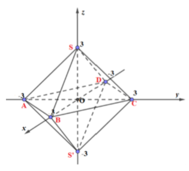
Các mặt chắn này cắt các trục Ox, Oy, Oz tại các điểm , A − 3 ; 0 ; 0 , B 3 ; 0 ; 0 , C 0 ; − 3 ; 0 D 0 ; 3 ; 0 , E 0 ; 0 ; − 3 , F 0 ; 0 ; 3 .
Từ đó, tập hợp các điểm M x ; y ; z thỏa mãn x + y + z = 3 là các mặt bên của bát diện đều x + y + z = 3 (hình vẽ) cạnh bằng 3 2 .
Thể tích khối bát diện đều là V = 3 2 3 . 2 3 = 36 (đvtt).
PT
1
CM
1 tháng 3 2018
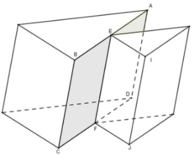
Ví dụ, hình sau được tạo bởi các đa giác nhưng không phải là một đa diện. Vì EF là giao của hai đa giác ABCD và EFJI nhưng nó không phải là cạnh chung của hai đa giác đó.
CM
16 tháng 11 2017
Chọn B.
Phương pháp:
Hình đa diện được lập thành là hình bát diện đều.
Cách giải:
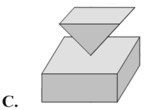
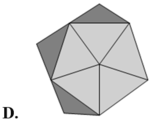
Hình đa diện có tính chất: Mỗi cạnh của đa giác nào cũng là cạnh chung của đúng hai đa giác
Nhưng hình 1.8c có cạnh AB là cạnh chung có 4 đa giác (không thỏa mãn t/c)