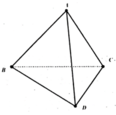
Cho tam giác ABC vuông tại B. Một đoạn thẳng AD vuông góc với mặt phẳng (ABC). Chứng minh rằng mặt phẳng (ABD) vuông góc với mặt phẳng (BCD).
Từ điểm A trong mặt phẳng (ABD) ta vẽ AH vuông góc với BD, chứng minh rằng AH vuông góc với mặt phẳng (BCD).


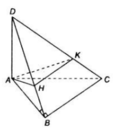

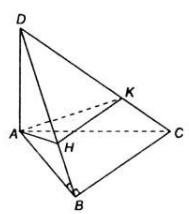


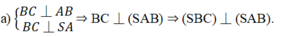
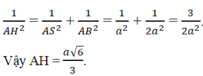
Vì AD ⊥ (ABC) nên AD ⊥ BC
Ngoài ra BC ⊥ AB nên ta có BC ⊥ (ABD)
Vì mặt phẳng (BCD) chứa BC mà BC ⊥ (ABD) nên ta suy ra mặt phẳng (BCD) vuông góc với mặt phẳng (ABD).
Hai mặt phẳng (BCD) và (ABD) vuông góc với nhau và có giao tuyến là BD. Đường thẳng AH thuộc mặt phẳng (ABD) và vuông góc với giao tuyến BD nên AH vuông góc với mặt phẳng (BCD).