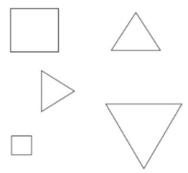
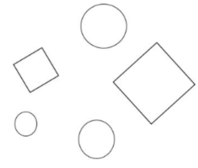
Tô màu vào các hình: cùng hình dạng thì tô cùng một màu.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Phương pháp giải:
Trong mỗi hình vuông nhỏ, tìm các hình tam giác và tứ giác rồi tô màu theo yêu cầu đề bài.
Chú ý : Ba hình đặt kề nhau thì có ba màu khác nhau.
Lời giải chi tiết:

a) Tô màu đỏ vào hình vuông. Tô màu xanh vào phần còn lại của hình tròn.
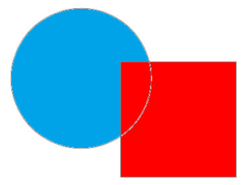
b) Viết tiếp vào chỗ chấm :
+ Hình vuông đặt trên hình tròn
+ Hình tròn đặt dưới hình vuông.

Đáp án A
TH1: 4 cạnh với 4 màu khác nhau, có A 6 4 = 360 cách.
TH2: 4 cạnh với 3 màu khác nhau, vì 2 cạnh giống màu không được kề nhau nên có 2 cách đặt vị trí cho 2 giống màu (đặt ở vị trí đối diện nhau). Tiếp theo, có 2! cách cho 2 màu còn lại. Vậy có C 6 3 . 3 .2.2 ! = 240
TH3: 4 cạnh với 2 màu khác nhau (giả sử xanh và đỏ), có 2 cách tô (AB=CD=xanh và AD=BC=đỏ/ hoặc AB=CD=đỏ và AD=BC=xanh) Trong trường hợp này có C 6 2 . 2 = 30 cách.
Vậy có tất cả 360 + 240 + 30 = 630 cách.

Đáp án D
Chú ý 4 cạnh khác nhau
Có C 6 4 cách chọn 4 màu khác nhau. Từ mỗi bộ 4 màu thì có 4 ! = 24 cách tô màu khác nhau
Có C 6 3 cách chọn 3 màu khác nhau. Từ mỗi bộ 3 màu, có 4.3 = 12 cách tô
Có C 6 2 cách chọn 2 màu khác nhau khi đó có: 2.1 = 2 cách tô
Tổng cộng: 24. C 6 4 + 4.3 C 6 3 + 2. C 6 2 = 630 cách

Đáp án D
Chú ý 4 cạnh khác nhau
Có C 6 4 cách chọn 4 màu khác nhau. Từ mỗi bộ 4 màu thì có 4! = 24 cách tô màu khác nhau.
Có C 6 3 cách chọn 3 màu khác nhau. Từ mỗi bộ 3 màu, có 4.3 = 12 cách tô.
Có C 6 2 cách chọn 2 màu khác nhau khi đó có: 2.1 = 2 cách tô.
Tổng cộng: 24 . C 6 4 + 4 . 3 C 6 3 + 2 . C 6 2 = 630 cách.
Phương pháp giải