Hãy chứng minh Định lý 1.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


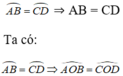
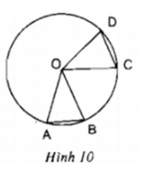
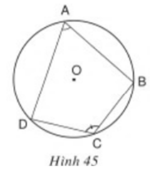
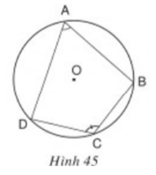
Xét ΔOAB và ΔOCD có:
OA = OC = R
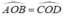
OB = OD = R
⇒ ΔOAB = ΔOCD (c.g.c)
⇒ AB = CD ( hai cạnh tương ứng)
AB = CD ⇒ 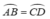
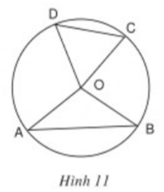
Xét ΔOAB và ΔOCD có:
OA = OC = R
AB = CD (gt)
OB = OD = R
⇒ ΔOAB = ΔOCD (c.c.c)
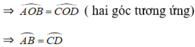

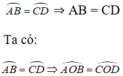
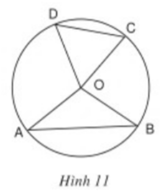
Xét ΔOAB và ΔOCD có:
OA = OC = R
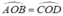
OB = OD = R
⇒ ΔOAB = ΔOCD (c.g.c)
⇒ AB = CD ( hai cạnh tương ứng)
b) AB = CD ⇒ 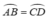
Xét ΔOAB và ΔOCD có:
OA = OC = R
AB = CD (gt)
OB = OD = R
⇒ ΔOAB = ΔOCD (c.c.c)
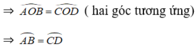

Theo tính chất góc nội tiếp chắn cung, ta có:
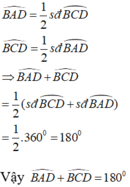
Vậy trong một tứ giác nội tiếp, tổng số đo hai góc đối nhau bằng 180o

Theo tính chất góc nội tiếp chắn cung, ta có:
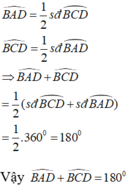
Vậy trong một tứ giác nội tiếp, tổng số đo hai góc đối nhau bằng 180 °


giả sử tam giác ABC có 2 đường trung tuyến BM và CN gặp nhau ở G
=> G là trong tâm của tam giác
-> GB=BM ; GC = CN
mà BM=CN (gt) nên GB = GC
=> tam giác GBC cân tại G
Do đó tam giác BCN=tam giác CBM vì:
BC là cạnh chung
CN = BM (gt)
=> tam giác ABC cân tại A
xét tam giác ABD và ACE :
E=D (=90o)
CE=BD (gt)
A:chung
suy ra tam giác ABD =ACE(ch_gn)
suy ra góc B=C(t/ư)
xét tam giác EIB&DIC:
E=D(=90o)
IE=ID
B=C
suy ra tam giácEIB=DIC
suy ra IB=IC
suy ra tam giác BIC cân tại I, suy ra B=C
suy ra:đpcm
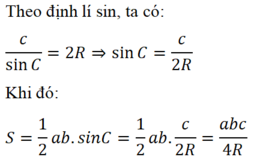
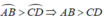

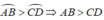
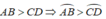
Vì F(x) là nguyên hàm của f(x) trên K nên (F(x))' = f(x). Vì C là hằng số nên (C)’ = 0.
Ta có:
(G(x))' = (F(x) + C)' = (F(x))' + (C)' = f(x) + 0 = f(x)
Vậy G(x) là một nguyên hàm của f(x).