Tính diện tích phần tô đậm, AB = FH = HE = GC = 1/2 DG và E, F là trung điểm của AD và BC. (Xem hình vẽ). Biết diện tích hình EHGD là 3cm2. Tìm diện tích hình thang ABCD.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan

CM
27 tháng 4 2018
Gọi điểm K nằm ở trung điểm DG. Nối BH, EK, KH, FG => Hình thang ABCD được chia thành 8 tam giác có diện tích bằng nhau. Mà S(EHGD) = 3 c m 2 ứng với 3 tam giác => S(ABCD) = 3:3 x 8 = 8 c m 2

2 tháng 3 2023
a: \(S_{AMB}=\dfrac{1}{2}\cdot6\cdot4=2\cdot6=12\left(cm^2\right)\)
\(S_{MBC}=\dfrac{1}{2}\cdot4\cdot12=2\cdot12=24\left(cm^2\right)\)
b: \(S_{ABCD}=\dfrac{1}{2}\cdot8\cdot\left(6+12\right)=4\cdot18=72\left(cm^2\right)\)

KV
27 tháng 8 2023
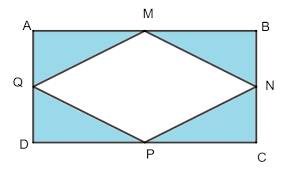
BC = 18 × 2/3 = 12 (cm)
Diện tích hình thoi MNPQ:
18 × 12 : 2 = 108 (cm²)
Diện tích hình chữ nhật ABCD:
18 × 12 = 216 (cm²)
Diện tích phần tô đậm:
216 - 108 = 108 (cm²)
Cách 1:
Gọi điểm K nằm ở trung điểm DG.
Nối BH, EK, KH, FG
=> Hình thang ABCD được chia thành 8 tam giác có diện tích bằng nhau.
Mà S(EHGD) = 3cm2 ứng với 3 tam giác
=> S(ABCD) = 3:3 x 8 = 8 cm2
Cách 2: Coi độ dài cạnh AB = FH = HE = GC = a
=> DG = 2xa
Coi chiều cao của hình EHGD là h thì đường cao của hình thang ABCD là 2 x h
S(EHGD) = ( a x 2 + a) x h x 1/2 = a x 3 x h x 1/2
S(ABCD) = [ ( a x 2 + a ) + a] x h x 2 x 1/2 = a x 8 x h x 1/2
=> Tỉ số S(EHGD) / S(ABCD) = a x 3 x h x 1/2 / a x 8 x h x 1/2 = 3/8
=> S(ABCD) = 3 : 3/8 = 8 cm2