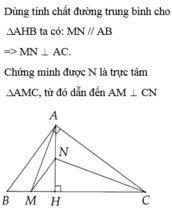
Cho tam giác ABC vuông tại A, kẻ đường cao AH. Gọi M, N lần lượt là trung điểm của HB, HA. Chứng minh AM vuông góc với CN.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
8 tháng 10 2018
Đúng(0)
Những câu hỏi liên quan
22 tháng 7 2020
Gọi gđ của ED và HA là O . Ta có:
tam giác MEH cân => góc HEM=MHE
tam giác OEH cân => góc OEH=OHE
mà góc OHE+MHE=90 độ
=> góc HEM+OEH=90 độ
=> EM vuông góc với ED
DN vuông góc với ED => DEMN là hình thang vuông
30 tháng 12 2021
a: Xét tứ giác AEHF có
\(\widehat{AEH}=\widehat{AFH}=\widehat{FAE}=90^0\)
Do đó: AEHF là hình chữ nhật
Suy ra: AH=FE
7 tháng 4 2022
a: Xét ΔAHB vuông tại H và ΔCHA vuông tại H có
\(\widehat{HAB}=\widehat{HCA}\)
Do đó: ΔAHB\(\sim\)ΔCHA
b: BM/AN=HB/HA
mà HB/HA=AB/CA
nên BM/AN=AB/CA
Xét ΔABM và ΔCAN có
BM/AN=AB/CA
\(\widehat{ABM}=\widehat{CAN}\)
Do đó: ΔABM\(\sim\)ΔCAN
10 tháng 7 2021
a) Xét tứ giác AEHF có
\(\widehat{FAE}=90^0\)
\(\widehat{AFH}=90^0\)
\(\widehat{AEH}=90^0\)
Do đó: AEHF là hình chữ nhật(Dấu hiệu nhận biết hình chữ nhật)
b) Ta có: ΔEHB vuông tại E(gt)
mà EN là đường trung tuyến ứng với cạnh huyền HB(N là trung điểm của HB)
nên \(EN=\dfrac{HB}{2}\)(Định lí 1 về áp dụng hình chữ nhật vào tam giác vuông)
24 tháng 7 2020
Bài làm
a) Vì \(\widehat{BAC}=\widehat{AEH}=\widehat{ADH}=90^0\)
=> tứ giác AEDH là hình chữ nhật.
=> Hai đường chéo AH và ED cắt nhau tại trung điểm mỗi đường. Mà AH = ED ( tính chất đường chéo của hình vuông )
Gọi giao điểm của AH và ED là O
=> Tam giác OHD cân tại O.
=> \(\widehat{AHD}=\widehat{EDH}\) (1)
Mà tam giác DHC vuông tại D
Mà DN là đường trung tuyến ( do N là trung điểm HC )
=> DN = HN = HC
=> Tam giác DHN cân tại N
=> \(\widehat{DHN}=\widehat{HDN}\)( hai góc ở đáy tam giác cân ) (2)
Cộng (1) vào (2), ta được: \(\widehat{AHD}+\widehat{DHN}=\widehat{EDH}+\widehat{HDN}\)
=> \(\widehat{AHC}=\widehat{EDN}\)
hay \(90^0=\widehat{EDN}\)
=> DN vuông góc với ED (3)
Vì tam giác OEH cân tại O ( cmt )
=> \(\widehat{OEH}=\widehat{OHE}\)( hai góc ở đáy tam giác cân ) (4)
Mà tam giác BEH vuông tại H
Mà EM là trung tuyến ( Do N là trung điểm BH )
=> EM = BM = MH
=> Tam giác EMH cân tại M.
=> \(\widehat{MEH}=\widehat{MHE}\) (5)
Cộng (4) và (5) ta được: \(\widehat{OEH}+\widehat{MEH}=\widehat{OHE}+\widehat{MHE}\)
=> \(\widehat{OEM}=\widehat{OHM}\)
hoặc \(\widehat{DEM}=\widehat{AHB}\)
hay \(\widehat{DEM}=90^0\)
=> ME vuông góc với ED (6)
Từ (3) và (6) => ME // DN
=> DEMN là hình thang
Mà \(\widehat{DEM}=90^0\)( cmg )
=> Hình thang DEMN là hình thang vuông ( đpcm )
KV
22 tháng 10 2023
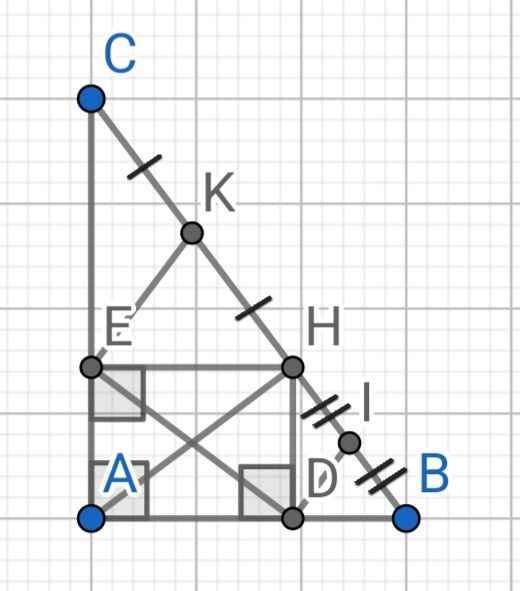a) Tứ giác ADHE có:
∠AEH = ∠ADH = ∠HAE = 90⁰ (gt)
⇒ ADHE là hình chữ nhật
⇒ AH = DE
b) BHD vuông tại D
I là trung điểm của HB (gt)
⇒ ID = IH = BH : 2
⇒ ∆IDH cân tại I
⇒ ∠IDH = ∠IHD
⇒ ∠HID = 180⁰ - (∠IDH + ∠IHD)
= 180⁰ - 2∠IHD (1)
∆CEH vuông tại E
K là trung điểm HC (gt)
⇒ KE = KC = HC : 2
⇒ ∆KEC cân tại K
⇒ ∠KEC = ∠KCE
⇒ ∠CKE = 180⁰ - (∠KEC + ∠KCE)
= 180⁰ - 2∠KEC (2)
Do HD ⊥ AB (gt)
AC ⊥ AB (gt)
⇒ HD // AC
⇒ ∠IHD = ∠KCE (đồng vị)
⇒ 2∠IHD = 2∠KCE (3)
Từ (1), (2) và (3) ⇒ ∠CKE = ∠HID
Mà ∠CKE và ∠HID là hai góc đồng vị
⇒ DI // KE