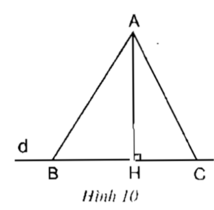
Cho hình 10. Hãy sử dụng định lí Py-ta-go để suy ra rằng:
Nếu HB > HC thì AB > AC;
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
13 tháng 2 2019
- Nếu HB = HC ⇒ HB2 = HC2.
⇒ AH2 + HB2 = AH2 + HC2
Kết hợp với 2 điều kiện (1) và (2)
⇒ AB2 = AC2
⇒ AB = AC
- Nếu AB = AC ⇒ AB2 = AC2
Kết hợp với 2 điều kiện (1) và (2)
⇒ AH2 + HB2 = AH2 + HC2
⇒ HB2 = HC2
⇒ HB = HC
PT
1
CM
23 tháng 9 2017
AB > AC ⇒ AB2 > AC2
Kết hợp với 2 điều kiện (1) và (2)
⇒ AH2 + HB2 > AH2 + HC2
⇒ HB2 > HC2
⇒ HB > HC
NT
Cho hình AH = 12cm, BH = 5cm, AC = 15cm. Tính AB, HC
. Dùng phương pháp áp dụng định lí Py - ta - go
0
8 tháng 4 2021
A B C H
Theo định lý Pytago ta có:
\(AB^2=BH^2+AH^2\)
\(AC^2=CH^2+AH^2\)
Vì \(BH< CH\Leftrightarrow BH^2< CH^2\Leftrightarrow BH^2+AH^2< CH^2+AH^2\)
\(\Rightarrow AB^2< AC^2\Rightarrow AB< AC\)
=> đpcm
19 tháng 4 2017
a) AB > AH; AC > AH.
b) Nếu HB > HC thì AB > AC.
hoặc có thể HB < HC thì AB < AC.
c) Nếu AB > AC thì HB > HC.
hoặc có thể AB < AC thì HB < HC.
19 tháng 4 2017
Trả lời
a) AB > AH; AC > AH.
b) Nếu HB > HC thì AB > AC.
hoặc có thể HB < HC thì AB < AC.
c) Nếu AB > AC thì HB > HC.
hoặc có thể AB < AC thì HB < HC.
18 tháng 5 2022
a: Do AC > A'C' nên lấy được điểm C1 trên cạnh AC sao cho AC1=A′C′.
Ta có ΔABC1=ΔA'B'C'
Suy ra B′C′=BC1
Mặt khác hai đường xiên BC và BC1 kẻ từ B đến đường thẳng AC lần lượt có hình chiếu trên AC là AC và AC1.
Vì AC > AC1 nên BC > BC1.
Suy ra BC > B'C'.
b:
-Giả sử AC<A'C'.
Khi đó theo chứng minh câu a) ta có BC < B'C'. Điều này không đúng với giả thiết BC > B'C'.
Giả sử AC=A'C'. Khi đó ta có ΔABC=ΔA'B'C' (c.g.c).
Suy ra BC=B'C'.
Điều này cũng không đúng với giả thiết BC>B'C'. Vậy ta phải có AC>A'C'.
30 tháng 6 2016
a) AB.>..AH; AC.>..AH
b) Nếu HB..>.HC thì AB.>..AC
Nếu HB..<.HC thì AB.<..AC
c) Nếu AB.<..AC thì HB.<..HC
Nếu AB.>..AC thì HB..>.HC
13 tháng 6 2020
tròn 1 điểm:33333 chế lại làm theo định lý pytago
ta có BH^2=AB^2-AH^2( áp dụng định lý pytago)
HC^2=AC^2-AH^2( áp dụng định lý pytago)
vì AB>AC=> AB^2>AC^2=> AB^2-AH^2>AC^2-AH^2=> BH^2>HC^2 => BH>CH (BH,CH>0)
làm thêm thui chứ cách của bạn ngắn hơn và đúng:33333
Xét tam giác AHB vuông tại H
Áp dụng định lí Py-ta-go ta có:
AB2 = AH2 + HB2 (1)
Xét tam giác AHC vuông tại H
Áp dụng định lí Py-ta-go ta có:
AC2 = AH2 + HC2 (2)
Nếu HB > HC ⇒ HB2 > HC2.
⇒ AH2 + HB2 > AH2 + HC2
Kết hợp với 2 điều kiện (1) và (2)
⇒ AB2 > AC2
⇒ AB > AC