Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a.
a) Hãy xác định đường vuông góc chung của hai đường thẳng chéo nhau BD' và B'C.
b) Tính khoảng cách của hai đường thẳng BD' và B'C
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
24 tháng 8 2019
Đáp án D.
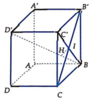
Cách 1: Gọi I là giao điểm của BC' và B'C . Trong B C ' D ' kẻ I H ⊥ B D ' tại H.
Ta có
B C ' ⊥ B ' C D ' C ' ⊥ B ' C B C ' , D ' C ' ∈ B C ' D ' ⇒ B ' C ⊥ B C ' D ' ⇒ B ' C ⊥ I H
Suy ra IH là đường vuông góc chung của BD' và B ' C ⇒ d B D ' , B ' C = I H .
Hai tam giác vuông BC'D' và BHI đồng dạng
⇒ I H D ' C ' = B I B D ' = a 2 2 a 3 = 6 6 ⇒ I H = a 6 6
Ta chọn D.
Cách 2: (Tọa độ hóa . Độc giả tự thực hiện)
CM
4 tháng 9 2017
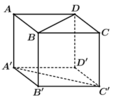
Ta có khoảng cách giữa hai đường thẳng chéo nhau BD và A'C' bằng khoảng cách giữa mặt phẳng song song (ABCD) và (A'B'C'D') thứ tự chứa BD và A'C' (hình vẽ). Do đó khoảng cách giữa hai đường thẳng BD và A'C' bằng a Chọn A.
CM
18 tháng 2 2019
Chọn A.
Ta có
A B C D / / A ' B ' C ' D B D ⊂ A B C D A ' C ' ⊂ A ' B ' C ' D ' ⇒ d B D ; A ' C ' = d A B C D ; A ' B ' C ' D ' = A A ' = a
a) Ta có:
Gọi I là tâm hình vuông BCC'B'
Trong mặt phẳng (BC'D') vẽ IK ⊥ BD' tại K
Ta có IK là đường vuông góc chung của BD' và B'C
b) Gọi O là trung điểm của BD'
Tam giác BC’D’ có OI là đường trung bình nên :
Vì ΔIOB vuông tại I có đường cao IK nên: