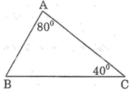
So sánh các cạnh của tam giác ABC biết rằng ∠A = 80o, ∠C = 40o
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


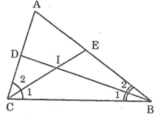
∠B = 80o, ∠C = 40o
Ta có:
∠(B1) = (1/2)∠(ABC) = (1/2).80o = 40o (vì BD là tia phân giác ∠(ABC))
∠(C1) = (1/2)∠(ACB) = (1/2).40o = 20o (vì CE là tia phân giác ∠(ACB))
Trong ΔIBC, ta có: ∠(BIC) + ∠(B1) + ∠(C1) = 180o(tổng 3 góc trong tam giác)
Vậy: ∠(BIC) = 180o - (∠(B1) + ∠(C1)) = 180o - (40o + 20o) = 120o

b. Khi ∠B = 30o thì ∠C = 180o - 30o - 80o = 70o ( 1 điểm )
Vì ∠B < ∠C < ∠A ⇒ AC < AB < BC ( 1 điểm )

Tam giác ABC cân tại A có ∠C = ∠B = 40o, ∠A = 100o
Vì B = C < A ⇒ AC = AB < BC. Chọn B

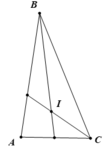
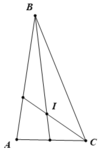
Trên BC lấy điểm E sao cho \(AB=BE\)
Dễ dàng chứng minh được \(\Delta ABD=\Delta EBD\left(c.g.c\right)\)
Do đó \(\widehat{BAC}=\widehat{BED}=80^0\)
Mà \(\widehat{BED}\) là góc ngoài tam giác DEC
\(\Rightarrow\widehat{BED}=\widehat{EDC}+\widehat{BCA}\\ \Rightarrow80^0=\widehat{EDC}+40^0\\ \Rightarrow\widehat{EDC}=40^0\Rightarrow\widehat{EDC}=\widehat{ECD}\left(=40^0\right)\\ \Rightarrow\Delta EDC.cân.tại.E\Rightarrow DE=EC\)
Vậy \(AB+AD=BE+EC=BC\)

b. Khi ∠B = 30o thì ∠C = 180o - 30o - 80o = 70o ( 1 điểm )
Vì ∠B < ∠C < ∠A ⇒ AC < AB < BC ( 1 điểm )

Theo giả thiết, tam giác cân này có một góc ngoài bằng 40o nên nó có một góc trong bằng 180o - 40o = 140o. Góc trong này không thể là góc ở đáy của tam giác cân mà phải là góc ở đỉnh. Vậy cạnh đáy của tam giác cân lớn hơn hai cạnh bên của nó.

Ta có ∠C = 180o - 80o - 30o = 70o
Vì A > C > B ⇒ BC > AB > AC. Chọn D

Ta có: ∠C = 180o - 40o - 25o = 115o
Vì ∠C > ∠A > ∠B ⇒ AB > BC > AC. Chọn B
Ta có: ∠A + ∠B + ∠C = 180o (tổng ba góc trong tam giác)
Suy ra: ∠B = 180o - (∠A + ∠C )
= 180o - (80o + 40o) = 60o
Trong ΔABC, ta có: ∠A > ∠B > ∠C
Suy ra: BC > AC > AB (đối diện với góc lớn hơn là cạnh lớn hơn).