Ba điện tích điểm q 1 = q 2 = q 3 = 1 , 6 . 10 - 19 C đặt trong chân không tại ba đỉnh tam giác đều cạnh a = 16 cm. Xác lực điện trường tổng hợp của hai điện tích q 1 và q 2 tác dụng lên q 3 .
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


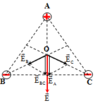
E → O = E → A + E → B + E → C = E → A + E → B C → E → A ↑ ↑ E → B C E O = E A + E B C
Trong đó: E A = E B C = k q O A 2 → O A = 2 3 a 2 − a 2 2 = 9.10 3 V m
→ E → A ↑ ↑ E → B C E O = E A + E B C = 18.10 3

Gọi \(\overrightarrow{E_1},\overrightarrow{E_2}\) là các vectơ cường độ điện trường gây ra bởi \(q_1\) và \(q_2\)
Ta có: \(E_1=E_2=k.\dfrac{q_1}{AB^2}=9.10^9.\dfrac{5.10^{-16}}{0,08^2}=7,03125.10^{-4}\left(V\text{/}m\right)\)
Từ hình vẽ: \(\left(\overrightarrow{E_1,}\overrightarrow{E_2}\right)=60^o\Rightarrow E=\sqrt{2E_1^2+2E_1^2.cos60^o}=E_1\sqrt{3}=7,03125.\sqrt{3}.10^{-4}\left(V\text{/}m\right)\)

a, 
khoảng từ tâm D đến các cạnh \(r=\dfrac{2}{3}.\sqrt{6^2-3^2}=2\sqrt{3}\)
ta có\(F_1=F_2=F_3=k\dfrac{\left|q_1.q_0\right|}{\left(2\sqrt{3}.10^{-2}\right)^2}=7,5\left(N\right)\)
ta tổng lực F2 và F3 với cosa=120 độ
\(F_{23}=\sqrt{F_2^2+F_3^2+2F_2F_3cos\alpha}=7,5\left(N\right)\)
theo phương chiều như hình vẽ ta có \(F=\left|F_{23}-F_1\right|=0\)

Lực điện tổng hợp tác dụng lên q 0 là: F → = F → 1 + F → 2 + F → 3 = F → 1 + F → 23
Trong đó: F 1 = k q 1 q 0 A O 2 = k q 1 q 0 2 3 a 3 2 2 = 3 k q 1 q 0 a 2 = 36.10 5
Vì BO = AO = CO nên q 1 = q 2 = q 3 → F 1 = F 2 = F 3
F → 2 ; F → 3 = 120 0 → F 1 = F 23
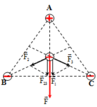
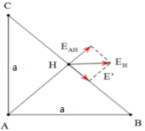
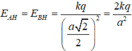

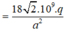

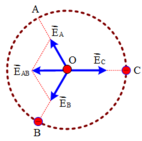
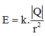
Các điện tích q 1 v à q 2 tác dụng lên điện tích q3 các lực F 1 → và F 2 → có phương chiều như hình vẽ:
Có độ lớn: F 1 = F 2 = k | q 1 q 3 | A C 2 = 9 . 10 9 . | 1 , 6.10 − 19 .1 , 6.10 − 19 | ( 16.10 − 2 ) 2 = 9 . 10 - 27 (N).
Lực tổng hợp do q 1 v à q 2 tác dụng lên q 3 là: F → = F 1 → + F 2 → ; có phương chiều như hình vẽ, có độ lớn: F = F 1 cos 30 ° + F 2 cos 30 ° = 2 F 1 cos 30 ° = 2 . 9 . 10 - 27 . 3 2 = 15 , 6 . 10 - 27 ( N )