Question

[Hoàng Đức Long]

Từ tầng dưới cùng của tòa nhà, một thang máy có khối lượng tổng cộng m = 1 tấn, đi lên tầng cao.

a. Trên đoạn đường s₁ = 5m đầu tiên, thang máy chuyển động nhanh dần và đạt vận tốc 5m/s. Tính công do động cơ thang máy thực hiện trên đoạn đường này.

b. Trên đoạn đường s₂ = 10m tiếp theo, thang máy chuyển động thẳng đều. Tính công suất của động cơ trên đoạn đường này.

c. Trên đoạn đường s₃ = 5m sau cùng, thang máy chuyển động chậm dần và dừng lại. Tính công của động cơ và lực trung bình do động cơ tác dụng lên thang máy trên đoạn đừng này. Lấy g = 10m/s².

Answer 1

[Vũ Thành Nam]

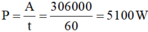
a, Ngoại lực tác dụng lên thang máy là trọng lực  và kéo  của động cơ thang máy. Áp dụng định lý về động năng ta có: W_đ1 – W_đ0 =  A F 1 → + A P 1 →

Mà W_đ1 = m . v 1 2 2 , W_đ0 = m . v 0 2 2 = 0  ;  

A P 1 → = − P . s 1 = − m . g . s 1 ( A P → 1 < 0 )

Vì thang máy đi lên

⇒ A F 1 = m . v 1 2 2 + m . g . s 1 = 1 2 .1000.5 2 + 1000.10.5 = 62500 J

b, Vì thang máy chuyển động đều, lực kéo của động cơ cân bằng với trọng lực  P → : F 2 → + P → = 0 . Công phát động của động cơ có độ lớn bằng công cản A F 2 → = − A P → với  A P = − P . s 2 = − m . g . s 2

=> A_F2 = mgs₂ do đó công suất của động cơ thang máy trên đoạn đường s₂ là: 

℘ 2 = A F 2 t = m . g . s 2 t = m . g . v 2 = m . g . v 1 ⇒ ℘ 2 = 1000.10.5 = 50000 ( W ) = 50 ( k W ) .

c, Ngoại lực tác dụng lên thang máy là trọng lực P → và lực kéo  F 3 →  của động cơ.

Áp dụng định lí động năng ta có: W_đ3 – W_đ2 = A_F3 + A_p’

Mà W_đ3 =  m . v 3 2 2 = 0 ;  W_đ2 = m v 2 2 2 (v₂ = v₁ = 5m/s);  A_p = - Ps₃ = - mgs₃

Công của động cơ trên đoạn đường s₃ là: A_F3 = mgs₃ -  m v 2 2 2   = 37500J

Áp dụng công thức tính công ta tìm được lực trung bình do động cơ tác dụng lên thang máy trên đoạn đường s₃:  F 3 ¯ = A F 3 s 3 = 37500 5 = 7500 N