Cho hàm số y = f(x) = 3x2 + 1. Tính
f 1 2 ; f 1 ; f 3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
4 tháng 9 2021
\(f\left(-1\right)=3\cdot\left(-1\right)^2-1=2\\ f\left(1\right)=3\cdot1^2-1=2\\ f\left(2\right)=3\cdot2^2-1=11\\ f\left(\dfrac{5}{2}\right)=3\cdot\left(\dfrac{5}{2}\right)^2-1=3\cdot\dfrac{25}{4}-1=\dfrac{71}{4}\)
4 tháng 9 2021
\(f\left(-1\right)=3\cdot1-1=2\)
\(f\left(1\right)=3\cdot1^2-1=2\)
\(F\left(2\right)=3\cdot2^2-1=11\)
\(f\left(\dfrac{5}{2}\right)=3\cdot\dfrac{25}{4}-1=\dfrac{71}{4}\)
D0
0
N
2
30 tháng 7 2023
1:
a: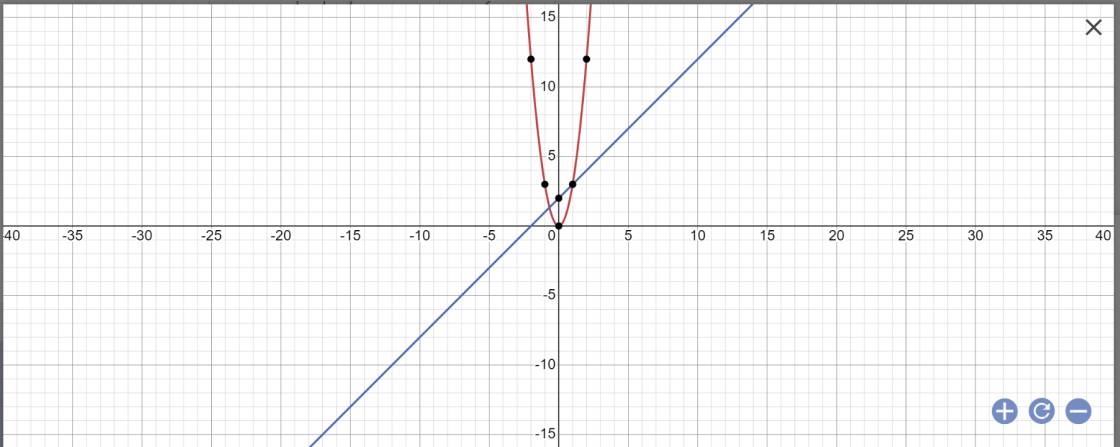 
b: PTHĐGĐ là:
3x^2-x-2=0
=>3x^2-3x+2x-2=0
=>(x-1)(3x+2)=0
=>x=1 hoặc x=-2/3
Khi x=1 thì y=3*1^2=3
Khi x=-2/3 thì y=3*4/9=4/3
c: f(-1)=3(-1)^2=3
f(2)=3*2^2=12
f(1/3)=3*(1/3)^2=1/3
PT
1
CM
2 tháng 9 2018
Ta có: f(-1) = 3.(-1)2 – 1 = 3.1- 1 = 2
f(-2) = 3.(-2)2 – 1 = 3.4 – 1 = 11
f(-3) = 3.(-3)2 – 1 = 3.9 – 1 = 26
f(0) = 3.02 - 1 = 0 - 1 = -1
Chọn (A).
Ta có y = f(x) = 3x2 + 1. Do đó: