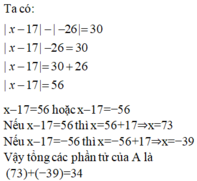Tập hợp các giá trị của thỏa...
Đọc tiếp
Tập hợp các giá trị của thỏa mãn
là
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
6 tháng 4 2016
vì a+c =9 nên để tổng abc+cba là số có 3 chử số thì tổng hàng chục b+b <10 nên b<5. vậy tập hợp A có 5 giá trị là 0,1,2,3,4
2 tháng 6 2016
abc + cba = 100a + 10b + c + 100c + 10b + a = 101a + 20b + 101c = 101(a + c) + 20b = 101.9 + 20b = 909 + 20b < 1000 (vì nó có 3 chữ số )
=> 20b < 1000 - 909 = 91 => b < \(\frac{91}{20}=4\frac{11}{20}\)
=> A = { b \(\in N\); b < \(4\frac{11}{20}\)} = { 0 ; 1 ; 2 ; 3 ; 4 } có 5 phần tử
16 tháng 7 2016
Theo đầu bài ta có:
abc + cba
= ( 100a + 10b + c ) + ( 100c + 10b + a )
= ( 100a + a ) + ( c + 100c ) + ( 10b + 10b )
= 101a + 101c + 20b
= 101 ( a + c ) + 20b
Do a + c = 9 nên:
= 101 * 9 + 20b
= 909 + 20b
- Do abc + cba là 1 số có 3 chữ số nên abc + cba < 1000 => 909 + 20b < 1000 => 20b < 91 => b < 4,55
- Do A là tập hợp các giá trị của chữ số b thỏa mãn điều kiện trên nên A = { 0 ; 1 ; 2 ; 3 ; 4 }
Vậy tập hợp A có 5 phần tử.
TN
1