Cho A = {x ∈ R: x + 2 ≥ 0}, B = {x ∈ R: 5 – x ≥ 0}. Khi đó A ∩ B là
A. [−2;5].
B. [−2;6].
C. [−5;2].
D. (−2;+ ∞ ).
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(A=[2;+\infty)\) ; \(B=\left(5;+\infty\right)\)
\(\Rightarrow B\backslash A=\varnothing\)

BPT thỏa mãn với mọi x khi và chỉ khi:
\(\left\{{}\begin{matrix}a-2b+1=0\\a^2-3b+2>0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}a=2b-1\\a^2-3b+2>0\end{matrix}\right.\)
\(\Rightarrow\left(2b-1\right)^2-3b+2>0\)
\(\Leftrightarrow4b^2-7b+3>0\)
\(\Rightarrow\left[{}\begin{matrix}b>1\\b< \dfrac{3}{4}\end{matrix}\right.\)

Tham khảo:
Ta có:
Bất phương trình \(1 - 2x \le 0\) có nghiệm là \(x \ge \frac{1}{2}\) hay \(A = [\frac{1}{2};+\infty)\)
Bất phương trình \(x - 2 < 0\) có nghiệm là \(x < 2\) hay \(B = ( - \infty ;2)\)
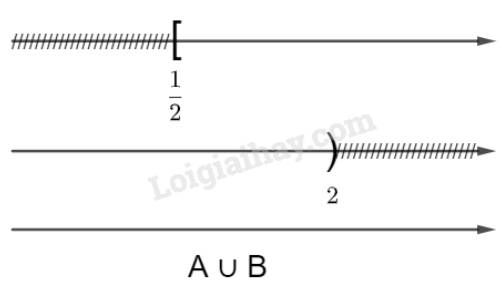
Vậy \(A \cup B = \mathbb R\)
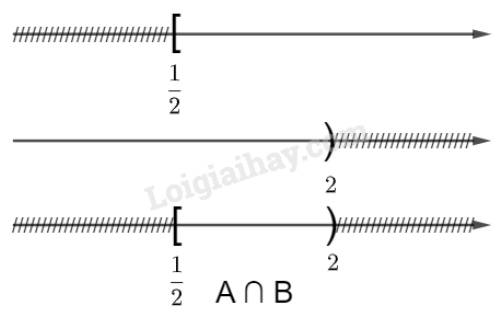
Vậy \(A \cap B = [\frac{1}{2};2)\)
Đáp án A