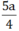Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Chọn C
Ba cạnh a, b, c ( a < b < c) của một tam giác theo thứ tự đó lập thành một cấp số cộng thỏa mãn yêu cầu thì:
a 2 + b 2 = c 2 a + b + c = 3 a + c = 2 b ⇔ a 2 + b 2 = c 2 3 b = 3 a + c = 2 b ⇔ a 2 + b 2 = c 2 b = 1 a = 2 b − c = 2 − c .
Ta có
a 2 + b 2 = c 2 → a = 2 − c b = 1 2 − c 2 + 1 = c 2
⇔ − 4 c + 5 = 0 ⇔ c = 5 4 ⇒ a = 3 4 b = 1 c = 5 4 .
Đáp án B
Ta sắp xếp các cạnh giá trị u 1 ; … u n tăng dần theo cấp số cộng là 3. Khi đó ta có:
S n = 158 u n = 44 ⇔ u 1 + 44 . n 2 = 158 u 1 + 3 n − 1 = 44 ⇔ u 1 = 47 − 3 n 47 − 3 n + 44 . n = 316 *
* ⇔ 3 n 2 − 91 n + 316 = 0 ⇔ n = 4 T M n = 79 3 L
Đáp án A
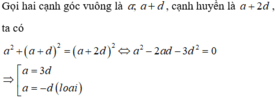
Do đó 3 cạnh của tam giác vuông cần tìm có dạng 3d ;4d ;5d, tức là một cạnh bất kì phải chia hết cho 3, hoặc chia hết cho 4, hoặc chia hết cho 5.
Trong các đáp án, chỉ có số 81 thỏa mãn chia hết cho 3.
Độ dài cạnh thứ ba là: (42 + 38) : 2 = 40 (dm)
Chu vi hình tam giác là: 42 + 38 + 40 = 120 (dm) = 1,2 dam
#lisa
Giải :
Độ dài cạnh thứ 3 là ( 42 + 38 ) : 2 = 40 ( dm)
Chu vi hình tam giác là : 42 + 38 + 40 = 120 ( dm ) = 1,2 dam
Một hình tam giác có độ dài hai cạnh là 12cm và 24cm. Biết độ dài cạnh thứ ba bằng trung bình cộng của độ dài hai cạnh kia. Hãy tính chu vi hình tam giác theo đơn vị m.
Chu vi hình tam giác là .....0,54........ m
Chọn C.
Gọi x, y, z theo thứ tự tăng dần của độ dài ba cạnh của tam giác.
Chu vi của tam giác: x + y + z = 3a (1)
Tính chất của cấp số cộng có x + z = 2y (2)
Vì tam giác vuông nên có: x2 + y2 = z2 (3)
Thay (2) vào (1) được 3y = 3a hay y = a, thay y = a vào (2) được: x + z = 2a hay x = 2a - z
Thay x và y vào (3) được: (2a – z)2 + a2 = z2 ⇔ 5a2 – 4az = 0 ⇔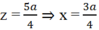
Độ dài ba cạnh của tam giác thỏa yêu cầu:
Vậy độ dài cạnh lớn nhất của tam giác là