Tính tổng tất cả các số hạng của một cấp số nhân , biết số hạng đầu bằng 18, số hạng thứ hai bằng 54 và số hạng cuối bằng 39366.
A. 19674.
B. 59040
C. 177138
D. 6552
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
28 tháng 5 2017
Chọn B.
u1 = 18, u2 = 54 ⇒ q = 3
un = 39366 ⇔ u1.qn-1 = 39366 ⇔ 18.3n-1 = 39366 ⇔ 3n-1 = 37 ⇔ n = 8.
Vậy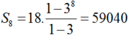 
HT
27 tháng 1 2021
Halo lau ko gap :)
\(\left\{{}\begin{matrix}u_1=\sqrt{2}\\u_2=u_1.q=-2\end{matrix}\right.\Rightarrow q=-\dfrac{2}{\sqrt{2}}=-\sqrt{2}\)
\(u_n=64\sqrt{2}=u_1.q^{n-1}\Leftrightarrow\sqrt{2}.\left(-\sqrt{2}\right)^{n-1}=64\sqrt{2}\)
\(\Leftrightarrow\left(-\sqrt{2}\right)^{n-1}=64\Rightarrow n-1=\log_{\sqrt{2}}64=12\Leftrightarrow n=13\)
\(S_{13}=u_1.\dfrac{q^{13}-1}{q-1}=\sqrt{2}.\dfrac{\left(-\sqrt{2}\right)^{13}-1}{-\sqrt{2}-1}=...\)
Check lại số má hộ tui nhó, số ghê quá
CM
1 tháng 12 2019
Chọn D
- Gọi u 1 , u 2 , . . . , u 7 là cấp số nhân cần tìm và q là công bội của cấp số nhân đó.
- Giả thiết ta có:
CM
25 tháng 5 2019
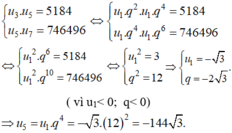
+ Gọi số hạng đầu của cấp số nhân là u1, công bội là x
Theo giả thiết ta có hệ phương trình
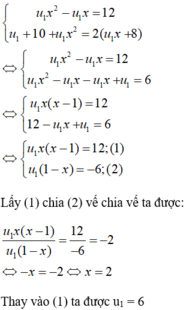
+ Tổng của năm số hạng đầu của CSN là:
CM
3 tháng 10 2018
Chọn D
Gọi 4 số phải tìm là a1, a2, a3, a4. Theo đầu bài Ta có hệ:
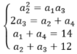
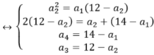
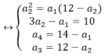
Giải các hệ phương trình Ta có kết quả a1=2, a2=4, a3=8 và a4=12
Chọn D
CM
20 tháng 11 2017
Kí hiệu u1,u2,u3,u4,u5 là các số hạng của cấp số nhân
Ta có :
Đáp án C
u 1 = 18 , u 2 = 54 ⇒ q = u 2 u 1 = 3.
Lại có u n = 39366 ⇔ u 1 . q n − 1 = 39366 ⇔ 18.3 n − 1 = 39366 ⇔ 3 n − 1 = 3 7 ⇔ n = 8
Vậy S 8 = 18. 1 − 3 8 1 − 3 = 59040
Chọn đáp án B.