Điều kiện của tham số m để phương trình sinx + (m+1)cosx = 2 vô nghiệm là:
A. m > 0
B.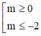 
C. 2 < m < 0
D. m <
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
30 tháng 5 2021
C1: \(a.sinx+b.cosx=c\)
Pt vô nghiệm \(\Leftrightarrow a^2+b^2< c^2\)
Bạn áp dụng công thức trên sẽ tìm ra m
C2: (Bạn vẽ đường tròn lượng giác sẽ tìm được)
Hàm số \(y=sinx\) đồng biến trên khoảng \(\left(-\dfrac{\pi}{2}+k2\pi;\dfrac{\pi}{2}+k2\pi\right)\) ( góc phần tư thứ IV và I)
Hàm nghịch biến trên khoảng \(\left(\dfrac{\pi}{2}+k2\pi;\dfrac{3\pi}{2}+k2\pi\right)\)( góc phần tư thứ II và III)
Ý A, khoảng nằm trong góc phần tư thứ III và thứ IV => Hàm nghịch biến sau đó đồng biến
Ý B, khoảng nằm trong góc phần tư thứ I và thứ II => hàm đồng biến sau đó nghịch biến
Ý C, khoảng nằm trong góc phần tư thứ IV; I ; II => hàm đồng biền sau đó nghịch biến
Ý D, khoảng nằm trong phần tư thứ IV ; I=> hàm đồng biến
Đ/A: Ý D
(Toi nghĩ thế)
HP
13 tháng 8 2021
1.
a, Phương trình có nghiệm khi:
\(\left(m+2\right)^2+m^2\ge4\)
\(\Leftrightarrow m^2+4m+4+m^2\ge4\)
\(\Leftrightarrow2m^2+4m\ge0\)
\(\Leftrightarrow\left[{}\begin{matrix}m\ge0\\m\le-2\end{matrix}\right.\)
b, Phương trình có nghiệm khi:
\(m^2+\left(m-1\right)^2\ge\left(2m+1\right)^2\)
\(\Leftrightarrow2m^2+6m\le0\)
\(\Leftrightarrow-3\le m\le0\)
HP
13 tháng 8 2021
2.
a, Phương trình vô nghiệm khi:
\(\left(2m-1\right)^2+\left(m-1\right)^2< \left(m-3\right)^2\)
\(\Leftrightarrow4m^2-4m+1+m^2-2m+1< m^2-6m+9\)
\(\Leftrightarrow4m^2-7< 0\)
\(\Leftrightarrow-\dfrac{\sqrt{7}}{2}< m< \dfrac{\sqrt{7}}{2}\)
b, \(2sinx+cosx=m\left(sinx-2cosx+3\right)\)
\(\Leftrightarrow\left(m-2\right)sinx-\left(2m+1\right)cosx=-3m\)
Phương trình vô nghiệm khi:
\(\left(m-2\right)^2+\left(2m+1\right)^2< 9m^2\)
\(\Leftrightarrow m^2-4m+4+4m^2+4m+1< 9m^2\)
\(\Leftrightarrow m^2-1>0\)
\(\Leftrightarrow\left[{}\begin{matrix}m>1\\m< -1\end{matrix}\right.\)
CM
13 tháng 11 2017
Phương trình (m + 2)x2 + 2x + m = 0 (a = m + 2; b = 2; c = m)
TH1: m + 2 = 0 ⇔ m = −2 ta có phương trình 2x – 2 = 0 ⇔ x = 1
TH2: m + 2 ≠ 0 ⇔ m ≠ −2
Ta có ∆ = 22 – 4(m + 2). m = −4m2 – 8m + 4
Để phương trình đã cho vô nghiệm thì:
m ≠ 2 − 4 m 2 − 8 m + 4 < 0 ⇔ m ≠ 2 2 − m + 1 2 < 0
⇔ m ≠ 2 m + 1 2 > 2 ⇔ m ≠ 2 m + 1 > 2 m + 1 < − 2
Đáp án cần chọn là: B
AH
Akai Haruma
Giáo viên
3 tháng 5 2023
Lời giải:
Để pt có 2 nghiệm phân biệt thì:
\(\left\{\begin{matrix}
m\neq 0\\
\Delta'=(-2)^2-m^2>0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix}
m\neq 0\\
(m-2)(m+2)<0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix}
m\neq 0\\
-2< m< 2\end{matrix}\right.\)
Đáp án A.
CM
27 tháng 1 2017
TH1: m = 0 ta có phương trình 4x + 5 = 0 ⇔ x = − 5 4
TH2: m ≠ 0
Ta có ∆ = [−2(m – 2)]2 – 4m (m + 5) = − 36m + 16
Để phương trình đã cho vô nghiệm thì:
m ≠ 0 − 36 m + 16 < 0 ⇔ m ≠ 0 36 m > 16
⇔ m ≠ 0 m > 8 19 ⇒ m > 8 19
Vậy với m > 8 19 thì phương trình đã cho vô nghiệm
Đáp án cần chọn là: A
LA
29 tháng 3 2022
a) 2x2 - 6x -1 = 0
delta phẩy = 9 + 2 = 11 = (\(\sqrt{11}\))2
x1 = \(\dfrac{3+\sqrt{11}}{2}\)
x2 = \(\dfrac{3-\sqrt{11}}{2}\)
b) xét delta phẩy có :
9 - 2.(2m-5) = 19 - 4m
+) điều kiện để phương trình vô nghiệm là 19 - 4m < 0 => m > \(\dfrac{19}{4}\)
+) điều kiện để phương trình có nghiệm kép là 19 - 4m = 0 => m = \(\dfrac{19}{4}\)
+) điều kiện để phương trình có 2 nghiệm phân biệt là 19 - 4m > 0
=> m < \(\dfrac{19}{4}\)
30 tháng 6 2020
phương trình vô nghiệm:
\(\Delta'< 0\Leftrightarrow\left(m+1\right)^2-4< 0\Leftrightarrow-2< m-1< 2\Leftrightarrow-1< m< 3\)
CM
29 tháng 6 2018
Phương trình 2x2 + 5x + m − 1 = 0 (a = 2; b = 5; c = m – 1)
⇒ ∆ = 52 – 4.2.(m – 1) = 25 – 8m + 8 = 33 – 8m
Để phương trình đã cho vô nghiệm thì
a ≠ 0 Δ < 0 ⇔ 2 ≠ 0 ( l d ) 33 − 8 m < 0 ⇔ m > 33 8
Vậy với m > 33 8 thì phương trình vô nghiệm.
Đáp án cần chọn là: D
Đáp án C
Phương pháp:
Phương trình bậc nhất đối với sin và cosasinx + bcosx = c vô nghiệm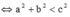
Cách giải: Phương trình sinx + (m+1)cosx = 2 vô nghiệm