Cho 8 quả cân có khối lượng lần lượt là 1 kg; 2 kg;…; 8 kg. Chọn ngẫu nhiên 3 quả cân. Tính xác suất để trọng lượng quả cân được chọn không quá 9 kg
A. 1 2
B. 1 4
C. 1 5
D. 1 8
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
29 tháng 10 2017
Đáp án D
Chọn ngẫu nhiên 3 quả cân từ 8 quả cân có 
cách.
Suy ra 
Gọi A là biến cố: “chọn được 3 quả cân có tổng khối lượng không quá 9kg”
Khi đó A={(1;2;3), (1;2;4), (1;2;6), (1;3;4), (1;3;5), (2;3;4)}
Suy ra n(A)=7
Vậy xác suất cần tìm là
14 tháng 8 2015
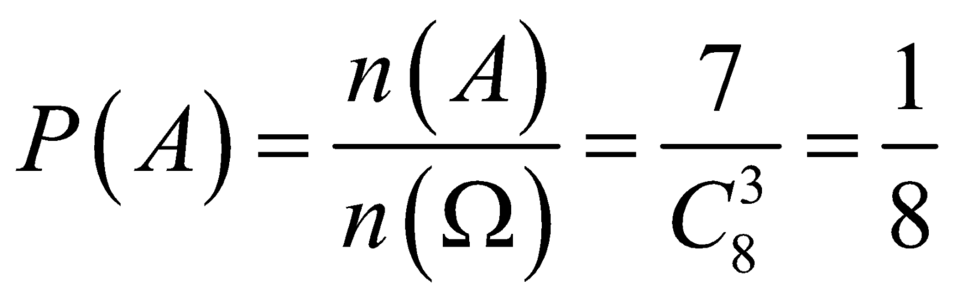
Đầu tiên,chia đôi 13kg gạo ra thành 2 phần bang nhau :1phan là 7kg & 6kg+1qua can
chia tiếp 6kg ra 2 phần bằng nhau nữa :3,5kg &2,5kg+1 quả cân
Bỏ qua căn bên phần thứ 2 đi là ra 2,5kg
CM
26 tháng 7 2019
Đáp án C
Các trường hợp thuận lợi là 6 ; 2 ; 1 , 5 ; 3 ; 1 , 5 ; 2 ; 1 , 4 ; 3 ; 2 , 4 ; 3 ; 1 , 4 ; 2 ; 1 , 3 ; 2 ; 1
Không gian mẫu Ω = C 8 3 = 56 ⇒ p = 7 56 = 1 8
CM
7 tháng 7 2017
Đáp án C
Các trường hợp thuận lợi là (6;2;1), (5;2;1), (5;2;1), (4;3;2), (4;3;1), (4;2;1), (3;2;1).
Không gian mẫu Ω = C 8 3 = 56 ⇒ p = 7 56 = 1 8 .
CM
23 tháng 10 2017
Đáp án C
Số phần tử của không gian mẫu là số các tổ hợp chập 3 của 8 phần tử
Gọi A là biến cố “Lấy được 3 quả cân có tổng trọng lượng không vượt quá 9kg”
n(A) = 7
Xác suất xảy ra biến cố A là:
P ( A ) = 7 56 = 1 8 a
Chọn ngẫu nhiên 3 quả cân từ 8 quả cân
Gọi A là biến cố: “chọn được 3 quả cân có tổng khối lượng không quá 9kg”
Khi đó A = {(1;2;3); (1;2;4); ( 1;2;5); (1;2;6); (1;3;4); (1;3;5); (2;3;4)}
Suy ra n(A) = 7
Vậy xác suất cần tìm là P A = n A n Ω = 7 C 8 3 = 1 8
Đáp án D