Tính:
a ) 0 , 1 2 b ) - o , 3 2 c ) - - 1 , 3 2 d ) - 0 , 4 - 0 , 4 2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
3 tháng 6 2018
Đúng(0)
Những câu hỏi liên quan
30 tháng 9 2021
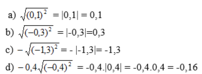
A=\(2^2-9^3+4^{-2}.16-2.5^2\)
\(=4-729+1-50=-774\)
B=\(\left(2^3.2\right).\dfrac{1}{2}+3^{-2}.3^2-7.1+5\)
\(B=2^4.\dfrac{1}{2}+1-7+5=8+1-7+5=7\)
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
16 tháng 8
C = 2-3 + (52)3.5-3 + 4-3.16 - 2.32 - 105.(\(\dfrac{24}{51}\))0
C = \(\dfrac{1}{8}\) + 56.5-3 + 4-3.42 - 2.9 - 105.1
C = \(\dfrac{1}{8}\) + 53 + \(\dfrac{1}{4}\) - 18 - 105
C = (\(\dfrac{1}{8}\) + \(\dfrac{1}{4}\)) - (105 - 125 + 18)
C = \(\dfrac{3}{8}\) - (-20 + 18)
C = \(\dfrac{3}{8}\) + 2
C = \(\dfrac{19}{8}\)
NV
26 tháng 6 2018
\(a,A=2^0+2^1+2^2+....+\)\(2^{2010}\)
\(\Rightarrow2A=2^1+2^2+2^3+....+2^{2011}\)
\(2A-A=\left(2^1+2^2+2^3+...+2^{2011}\right)-\left(2^0+2^1+2^2+...+2^{2010}\right)\)
\(A=2^{2011}-2^0\)
\(A=2^{2011}-1\)
\(b,B=1+3+3^2+...+3^{100}\)
\(\Rightarrow3B=3+3^2+3^3+...+3^{101}\)
\(3B-B=\left(3+3^2+3^3+...+3^{101}\right)-\left(1+3+3^2+...+3^{100}\right)\)
\(2B=3^{101}-1\)
\(\Rightarrow B=\frac{3^{101}-1}{2}\)
\(c,C=4+4^2+4^3+...+4^n\)
\(\Rightarrow4C=4^2+4^3+4^4+...+4^{n+1}\)
\(4C-C=\left(4^2+4^3+4^4+...+4^{n+1}\right)-\left(4+4^2+4^3+...+4^n\right)\)
\(3C=4^{n+1}-4\)
\(\Rightarrow C=\frac{4^{n+1}-4}{3}\)
\(d,D=1+5+5^2+...+5^{2000}\)
\(\Rightarrow5D=5+5^2+5^3+...+5^{2001}\)
\(5D-D=\left(5+5^2+5^3+...+5^{2001}\right)-\left(1+5+5^2+...+5^{2000}\right)\)
\(4D=5^{2001}-1\)
\(\Rightarrow D=\frac{5^{2001}-1}{4}\)
TC
21 tháng 3 2021
b)
B=1+3+3^2+3^3+..+3^100
=> 3B = 3 + 3^2 + 3^3 + ...+ 3^101
=> 3B - B = ( 3 + 3^2 + 3^3 + ...+ 3^101) - (1+3+3^2+3^3+..+3^100)
=> 2B = 3^101 - 1
=> B =( 3^101 - 1) / 2
HP
7 tháng 1 2017
1a) (x-2)(x+1)= 0
Suy ra \(\orbr{\begin{cases}x-2=0\\x+1=0\end{cases}}\)Suy ra \(\orbr{\begin{cases}x=2\\x=-1\end{cases}}\)
AH
Akai Haruma
Giáo viên
2 tháng 3 2020
Câu 1:
$x-2=0\Leftrightarrow 2(x-2)=0\Leftrightarrow 2x-4=0$
Đáp án B.
Câu 2:
Để PT đã cho có nghiệm $x=5$ thì $m(5-3)=6$
$\Leftrightarrow m=3$
Đáp án C
Câu 3:
Dựa vào khái niệm pt bậc nhất 1 ẩn. Đáp án B
Câu 4:
$2x-4=0\Leftrightarrow \frac{2x-4}{4}=0\Leftrightarrow \frac{x}{2}-1=0$
Đáp án D