Ở độ cao nào sau đây gia tốc rơi tự do chỉ bằng phân nửa gia tốc rơi trên mặt đất ? Cho bán kính trái đất bằng R = 6400km
A. h=2651km
B. h=9051km
C. h=15451km
D. h=4525,5km
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VT
6 tháng 1 2018
Chọn đáp án B
Ta có:
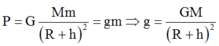
- Khi h = 0 thì :
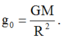
- Khi ở độ cao h thì :
30 tháng 11 2021
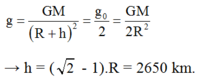
Tại mặt đất: \(g_0=G\cdot\dfrac{M}{R^2}\)
Tại độ cao h: \(g=G\cdot\dfrac{M}{\left(R+h\right)^2}\)
Xét tỉ lệ:
\(\dfrac{g_0}{g}=\dfrac{\left(R+h\right)^2}{R^2}=\dfrac{9,81}{4,9}=2\)
\(\Rightarrow\dfrac{\left(R+h\right)^2}{R^2}=2\Rightarrow h=2650,97km\)
25 tháng 7 2016
Tại mặt đất, gia tốc rơi tự do là:
\(g_0=\frac{GM}{R^2}=\left(1\right)\)
Tại độ cao h so với mặt đất, gia tốc rơi tự do là:
\(g_h=\frac{GM}{\left(R+h\right)^2}\left(2\right)\)
Từ (1) và (2) \(\rightarrow\frac{g_0}{g_h}=\frac{\left(R+h\right)^2}{R^2}=2\rightarrow h=\left(\sqrt{2}+1\right).R^{ }\)
Thay số : h = (1,41 - 1).6400 = 2624 (km)
13 tháng 11 2021
Tại mặt đất, gia tốc rơi tự do: \(g_0=\dfrac{GM}{R^2}\)
Ở độ cao h so với mặt đất, gia tốc rơi tự do của một vật là:
\(g_h=g_0\left(\dfrac{GM}{\left(R+h\right)^2}\right)\)
Từ hai công thức trên ta suy ra:
\(\dfrac{g_0}{g_h}=\dfrac{\left(R+h\right)^2}{R^2}=9\)
Chọn đáp án A
Gia tốc ở mặt dất và độ cao h: