Phần 1: Trắc nghiệmTrong các mệnh đề sau, mệnh đề nào là mệnh đề đúng? A. lim n → ∞ 1 n = 1 B. lim n → ∞...

K

Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn lớp

Chọn môn

Mua vip

PT

Pham Trong Bach

30 tháng 3 2019

Phần 1: Trắc nghiệmTrong các mệnh đề sau, mệnh đề nào là mệnh đề đúng? A. lim n → + ∞ 1 n = 1 B. lim n → + ∞ q n = 0 , q > 1 C. lim n → + ∞ 1 n = 0 D. lim n → + ∞ q n = 0 , q < 1 ...

#Toán lớp 11

1

CM

Cao Minh Tâm

30 tháng 3 2019

- Dựa vào một số giới hạn đặc biệt ta có:

Đề kiểm tra 45 phút Đại số 11 Chương 4 có đáp án (Đề 1)

→ ta có khẳng định D là đúng.

Chọn D.

Những câu hỏi liên quan

PT

Pham Trong Bach

15 tháng 8 2017

Phần I: Trắc nghiệmTrong các mệnh đề sau, mệnh đề nào là mệnh đề đúng? A. lim n → + ∞ - 2 n 2 = - 2 B. lim n → + ∞ q n = 0 , q < 1 C. lim n → + ∞ 1 n n = 0 D. lim n → + ∞ 2 n = 0 ...

#Toán lớp 11

1

CM

Cao Minh Tâm

15 tháng 8 2017

Dựa vào một số giới hạn đặc biệt ta có:

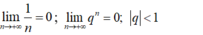
Đề kiểm tra 45 phút Đại số 11 Chương 4 có đáp án (Đề 2)

⇒ Mệnh đề C là đúng.

Chọn C.

PT

Pham Trong Bach

4 tháng 3 2019

Cho I n = ∫ 0 1 e - n x 1 + e - x d x n ∈ ℕ Đặt u n = ( I 1 + I 2 ) + 2 ( I 2 + I 3 ) + . . . . . + n ( I n + I n + 1 ) . Biết lim u n = L Mệnh đề nào sau...

#Toán lớp 12

1

CM

Cao Minh Tâm

4 tháng 3 2019

Đáp án B

PT

Pham Trong Bach

9 tháng 6 2018

Với k là số nguyên dương bất kỳ, xét các mệnh đề sau: 1. lim x → + ∞ 1 x k = + ∞ 2 . lim x → - ∞ 1 x k = 0 3 . lim x → + ∞ x k = + ∞ 4 . lim x → - ∞ x k = + ∞ n ế u ...

#Toán lớp 11

1

CM

Cao Minh Tâm

9 tháng 6 2018

DN

Duu nè

21 tháng 10 2021

Bài 4. Trong các mệnh đề sau, mệnh đề nào là đúng ? Giải thích ? Phát biểu các mệnh đề đó thành lời: a) x R x2    , 0. b) x R x x2    , c) x Q 2     ,4x 1 0 . d) n N n n 2    , . e) f) x R x x2 x R x x     ,5 3 1 2      , 1 0

#Toán lớp 10

0

LH

Lê Hồng Ngọc

27 tháng 8 2019 - olm

cho 3 mệnh đề sau, với n là số tự nhiên

(1) n+ 8 là số chính phương

(2) chữ số tận cùng của n là 4

(3) n-1 là số chính phương

biết hai mệnh đề đúng và 1 mệnh đề sai. hãy xác định mệnh đề nào đúng nào sai

#Toán lớp 10

1

S

★๖ۣۜßảo๖ۣۜPɦα♏๖ۣۜ[EηgĻïšħ☯€lub]★

27 tháng 8 2019

ta thấy 1 số chính phương không bao giờ có đuôi là 2;3;7;8

Mà nếu mệnh đề (2) đúng thì n+8=...2 => mệnh đề (1) sai và n-1=...3 => mệnh đề (3) sai

Nhưng chỉ có 1 mệnh đề sai nên chỉ có mệnh đề (2) là thỏa mãn

Vậy n+8 và n+1 là số chính phương

\(\Rightarrow\left(n+8\right)-\left(n-1\right)=9\)

\(\Leftrightarrow\left(n+8\right)^2-\left(n-1\right)^2=9^2\)

\(\Leftrightarrow\left[\left(n+8\right)-\left(n-1\right)\right]\left[\left(n+8\right)+\left(n-1\right)\right]=9^2\)

\(\Leftrightarrow9\left(2n+7\right)=9^2\)

\(\Leftrightarrow2n-7=9\)

\(\Leftrightarrow n=8\)

Vậy n=8 thì mới thỏa mãn mệnh đề (1) và (3)

NM

Nguyễn Minh Quân

14 tháng 9 2023

Trong các mệnh đề sau, mệnh đề nào đúng? Giải thích? Phát biểu các mệnh đề đó thành lờia) \(\exists x\in R\), 5x - \(3x^2\) \(\le1\)b) \(\exists x\in R\), \(x^2+2x+5\) là hợp sốc) \(\forall n\in N\), \(n^2+1\) không chia hết cho 3d) \(\forall n\in N^{sao}\), n ( n + 1 ) là số lẻe) \(\forall n\in N^{sao}\), n ( n + 1) ( n + 2 ) chia hết cho...

#Toán lớp 10

0

NM

Nguyễn Minh Quân

14 tháng 9 2023

Thanks bạn

PT

Pham Trong Bach

10 tháng 1 2017

Phần I: Trắc nghiệm Chọn mệnh đề đúng trong các mệnh đề sau: A. Hai đường thẳng không có điểm chung thì chéo nhau. B. Hai đường thẳng phân biệt không có điểm chung thì chéo nhau. C. Hai đường thẳng chéo nhau thì không có điểm chung. D. Hai đường thẳng lần lượt nằm trên hai mặt phẳng phân biệt thì chéo...

#Toán lớp 11

1

CM

Cao Minh Tâm

10 tháng 1 2017

Chọn C.

- Câu A sai vì hai đường thẳng không có điểm chung thì chéo nhau hoặc song song với nhau.

- Câu B sai vì hai đường thẳng phân biệt không có điểm chung thì chéo nhau hoặc song song với nhau.

- Câu D sai vì hai đường thẳng phân biệt nằm trên hai mặt phẳng phân biệt thì có thể chéo nhau hoặc song song với nhau.

NM

Nguyễn Minh Quân

28 tháng 9 2023

Trong các mệnh đề sau, mệnh đề nào đúng?A. \(\exists\in Q:9x^2-1=0\) B. \(\forall x\in R:x^2+2x+10\)C. \(\forall n\in N:n^2n\) D. \(\exists n\in...

#Toán lớp 10

1

MH

Minh Hiếu

28 tháng 9 2023

\(9x^2-1=0\)

\(x^2=\dfrac{1}{9}\)

\(\Rightarrow x=\pm\dfrac{1}{3}\Rightarrow x\in Q\)

Chọn A

T

Toru

28 tháng 9 2023

Thầy ơi nếu \(\forall n\in N:n^2>n\) mà với \(n=0;n=1\) thì mệnh đề \(C\) sai chứ ạ!

PT

Pham Trong Bach

24 tháng 12 2018

Hãy xem trong lời giải của bài toán sau đây có bước nào bị sai?Bài toán: chứng minh rằng với mọi số nguyên dương n, mệnh đề sau đây đúng:A(n) : “nếu a và b là những số nguyên dương mà max{a,b} = n thì a = b”Chứng minh :Bước 1: A(1):”nếu a,b là những số nguyên dương mà max{a,b} = 1 thì a = b”Mệnh đề A(1) đúng vì max{a,b} = 1 và a,b là những số nguyên dương thì a= b =1.Bước 2: giả sử A(k) là...

#Toán lớp 11

1

CM

Cao Minh Tâm

24 tháng 12 2018

Đáp án là C. Ta có a,b∈N* không suy ra a -1, b -1∈N* . Do vậy không áp dụng được giả thiết quy nạp cho cặp {a -1, b -1}.

Chú ý: nêu bài toán trên đúng thì ta suy ra mọi số tự nhiên đều bằng nhau. Điều này là vô lí.