Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a: Để (d)//(d') thì \(\left\{{}\begin{matrix}k-2=2\\-k\ne4\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}k=4\\k\ne-4\end{matrix}\right.\)
=>k=4
b: Để (d) vuông góc (d') thì \(2\left(k-2\right)=-1\)
=>2k-4=-1
=>2k=3
=>\(k=\dfrac{3}{2}\)
c: Để (d) cắt (d') thì \(k-2\ne2\)
=>\(k\ne4\)
Đường thẳng (d) có dạng \(y=kx+m\)
\(A\left(0;2\right)\in\left(d\right)\Rightarrow m=2\)
\(\Rightarrow y=kx+2\left(d\right)\)
\(\left(d\right)\) cắt \(\left(P\right)\) tại hai điểm phân biệt khi phương trình \(x^2+\left(4-k\right)x+1=0\) có hai nghiệm phân biệt
\(\Leftrightarrow\Delta=\left(k-2\right)\left(k-6\right)>0\)
\(\Leftrightarrow\left[{}\begin{matrix}k>6\\k< 2\end{matrix}\right.\)
Ta có \(x_1=\dfrac{k-4+\sqrt{k^2-8k+12}}{2}\Rightarrow y_1=\dfrac{k^2-4k+4+k\sqrt{k^2-8k+12}}{2}\)
\(\Rightarrow E\left(\dfrac{k-4+\sqrt{k^2-8k+12}}{2};\dfrac{k^2-4k+4+k\sqrt{k^2-8k+12}}{2}\right)\)
\(x_1=\dfrac{k-4-\sqrt{k^2-8k+12}}{2}\Rightarrow y_1=\dfrac{k^2-4k+4-k\sqrt{k^2-8k+12}}{2}\)
\(\Rightarrow F\left(\dfrac{k-4-\sqrt{k^2-8k+12}}{2};\dfrac{k^2-4k+4-k\sqrt{k^2-8k+12}}{2}\right)\)
Tọa độ trung điểm \(I\left(\dfrac{k-4}{2};\dfrac{k^2-4k+4}{2}\right)\)
\(x-2y+3=0\left(d'\right)\)
\(I\left(\dfrac{k-4}{2};\dfrac{k^2-4k+4}{2}\right)\in\left(d'\right)\Rightarrow\dfrac{k-4}{2}-\left(k^2-4k+4\right)+3=0\)
\(\Leftrightarrow2k^2-9k+6=0\)
\(\Leftrightarrow\left[{}\begin{matrix}k=\dfrac{9+\sqrt{33}}{2}\left(l\right)\\k=\dfrac{9-\sqrt{33}}{2}\left(tm\right)\end{matrix}\right.\)
\(\Leftrightarrow k=\dfrac{9-\sqrt{33}}{2}\)
P/s: Không biết đúng kh.
Đường thẳng d đi qua A và có hệ số góc k nên có dạng y= k( x+ 1) hay
Kx- y+k=0 .
Phương trình hoành độ giao điểm của C và d là:
x 3 - 3 x 2 + 4 = k x + k ⇔ ( x + 1 ) ( x 2 - 4 x + 4 - k ) = 0
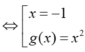
D cắt tại ba điểm phân biệt khi phương trình (*) có hai nghiệm phân biệt khác -1
⇔ ∆ ' > 0 g ( - 1 ) ≠ 0 ⇔ k > 0 k ≠ 9
Khi đó g( x) =0 khi x=2- k ; x = 2 + k Vậy các giao điểm của hai đồ thị lần lượt là
A ( - 1 ; 0 ) ; B ( 2 - k ; 3 k - k k ) ; C ( 2 + k ; 3 k + k k ) .
Tính được
B C = 2 k 1 + k 2 , d ( O , B C ) = d ( O , d ) = k 1 + k 2 .
Khi đó
S ∆ O B C = 1 2 . k k 2 + 1 . 2 k . k 2 + 1 = 1 ⇔ k k = 1 ⇔ k 3 = 1 ⇔ k = 1 .
Vậy k= 1 thỏa yêu cầu bài toán.
Chọn C.
Đáp án A
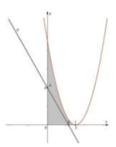
Phương trình hoành độ giao điểm của đồ thị hàm số y = x 2 − 6 x + 9 và trục hoành là:
x 2 − 6 x + 9 = 0 ⇔ x = 0 .
Diện tích hình phẳng (H) giới hạn bởi đồ thị hàm số y = x 2 − 6 x + 9 và 2 đường thẳng x= 0; y = 0 là:
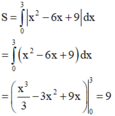
Phương trình đường thẳng (d) có hệ số góc k và cắt trục tung tại điểm A(0;4) là: y = kx +4
Gọi B là giao điểm của (d) và trục hoành ⇒ B − 4 k ; 0 .
Để (d) chia (H) thành 2 phần có diện tích bằng nhau thì:
.
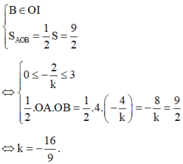Đường thẳng d có phương trình y = − k x + b ( k ≠ 0 ) có –k là hệ số góc
Đáp án cần chọn là: A