Cho tam giác ABC vuông tại A , đường cao AH (như hình vẽ). Hệ thức nào sau đây là sai?
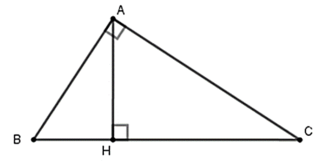
A. A B 2 = B H . B C
B. A C 2 = C H . B C
C. AB.AC = AH.BC
D. A H 2 = A B 2 + A C 2 A B 2 . A C 2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Cho tam giác ABC vuông tại A , đường cao AH. Khi đó ta có các hệ thức:
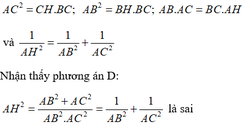

Nhận thấy ah = bc nên phương án C là sai
Đáp án cần chọn là: C

Cho tam giác ABC vuông tại A, đường cao AH. Khi đó ta có hệ thức
A C 2 = C H . B C ; A B 2 = B H . B C ; AB.AC = BC.AH và 1 A H 2 = 1 A B 2 + 1 A C 2
Nhận thấy phương án D: A H 2 = A B 2 + A C 2 A B 2 . A C 2 là sai
Đáp án cần chọn là: D

Đáp án B
Cho tam giác ABC vuông tại A , đường cao AH . Khi đó ta có hệ thức: A H 2 = BH.CH

Đáp án B
Cho tam giác ABC vuông tại A , đường cao AH. Khi đó ta có hệ thức: A H 2 = BH.CH

Cho tam giác ABC vuông tại A, đường cao AH. Khi đó ta có hệ thức:
HA2 = HB.HC
Đáp án cần chọn là: B

a2 = b2 + c2
b2 = a x b'
c2 = a x c'
h2 = b’ x c'
ah = b x c
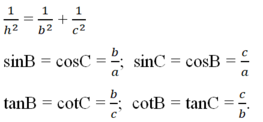

Xét ΔHBA vuông tại H và ΔHAC vuông tại H có
góc HBA=góc HAC
=>ΔHBA đồng dạng với ΔHAC
=>HB/HA=HA/HC
=>HA^2=HB*HC

Áp dụng HTL:
\(AB^2=BH\cdot BC\\ AC^2=CH\cdot BC\\ AH^2=BH\cdot HC\\ AB\cdot AC=AH\cdot BC\\ \dfrac{1}{AH^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}\\ AB^2+AC^2=BC^2\left(pytago\right)\)
Đáp án D
Cho tam giác ABC vuông tại A , đường cao AH. Khi đó ta có các hệ thức: