Phương trình 3 - x + 1 3 = x 4 + 1 có 1 nghiệm x = a b là phân số tối giản. Tính a + b
A. 22
B. 17
C. 27
D. 20
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
10 tháng 6 2017
Đáp án A.
Phương trình đã cho tương đương với:
2 x 2 + m x + 1 = x 2 + 6 x + 9 x ≥ − 3 ⇔ x 2 + m − 6 x − 8 = 0 1 x ≥ − 3
Để phương trình có hai nghiệm phân biệt thì (1) phải có 2 nghiệm phân biệt x 2 > x 1 ≥ − 3
⇔ Δ > 0 x 1 + x 2 ≥ − 6 x 1 + 3 x 2 + 3 ≥ 0 ⇔ m − 6 2 + 32 > 0 − m − 6 ≥ − 6 − 8 + 3. − m + 6 + 9 ≥ 0 ⇔ 6 − m ≥ − 6 19 − 3 m ≥ 0 ⇔ m ≤ 12 m ≤ 19 3 ⇔ m ≤ 19 3
Do đó
a b = 19 3 ⇒ a = 19 b = 3 ⇒ B = a 2 − b 3 = 19 2 − 3 3 = 334.
CM
22 tháng 10 2019
Điều kiện:
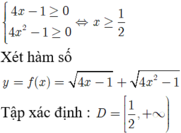
Đạo hàm
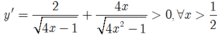
Suy ra hàm số đồng biến trên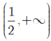 
Do đó : phương trình
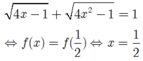
Chọn B.
CM
13 tháng 7 2019
a, Cách 1. Đặt 1 y + 1 = u ta được 3 x - 2 u = 1 5 x + 2 u = 3
Giải ra ta được x = 1 2 ; u = 1 4
Từ đó tìm được y = 3
Cách 2. Cộng vế với vế hai phương trình, ta được 8x = 4
Từ đó tìm được x = 1 2 và y = 3
b, Vì x1x2 = -m2 - 1 < 0 "m nên phương trình đã cho luôn có hai nghiệm phân biệt và trái dấu.
Cách 1. Giả sử x 1 < 0 < x 2
Từ giả thiết thu được – x 1 + x 2 = 2 2
Biến đổi thành x 1 + x 2 2 - 4 x 1 x 2 = 8
Áp dụng định lý Vi-ét, tìm được m = 1 hoặc m = - 3 5
Cách 2. Bình phương hai vế của giả thiết và biến đổi về dạng
x 1 + x 2 2 - 2 x 1 x 2 + 2 x 1 x 2 = 8
=> m - 1 2 + 4 m 2 + 1 = 8
Do x 1 x 2 = - x 1 x 2
Áp dụng hệ thức Vi-ét, ta cũng tìm được m = 1 hoặc m = - 3 5
AH
Akai Haruma
Giáo viên
15 tháng 3 2021
Lời giải:
a) Khi $m=1$ thì pt trở thành:
$x^2-2x-5=0$
$\Leftrightarrow (x-1)^2=6$
$\Rightarrow x=1\pm \sqrt{6}$
b) Để $x_1=3$ là nghiệm của pt thì:
$3^2-2.m.3+2m-7=0\Leftrightarrow m=\frac{1}{2}$
Nghiệm còn lại $x_2=(x_1+x_2)-x_1=2m-x_1=2.\frac{1}{2}-3=-2$
c)
$\Delta'= m^2-(2m-7)=(m-1)^2+6>0$ với mọi $m\in\mathbb{R}$ nên pt luôn có 2 nghiệm phân biệt $x_1,x_2$
Theo định lý Viet: $x_1+x_2=2m$ và $x_1x_2=2m-7$
Khi đó:
Để $x_1^2+x_2^2=13$
$\Leftrightarrow (x_1+x_2)^2-2x_1x_2=13$
$\Leftrightarrow (2m)^2-2(2m-7)=13$
$\Leftrightarrow 4m^2-4m+1=0\Leftrightarrow (2m-1)^2=0\Leftrightarrow m=\frac{1}{2}$
d)
$x_1^2+x_2^2+x_1x_2=(x_1+x_2)^2-x_1x_2$
$=(2m)^2-(2m-7)=4m^2-2m+7=(2m-\frac{1}{2})^2+\frac{27}{4}\geq \frac{27}{4}$
Vậy $x_1^2+x_2^2+x_1x_2$ đạt min bằng $\frac{27}{4}$. Giá trị này đạt tại $m=\frac{1}{4}$
Chọn đáp án C