Tứ giác nội tiếp là gì? s đ A B ⏜ = s đ A C ⏜ + s đ C B ⏜ ?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
19 tháng 7 2017
Đúng(0)
Những câu hỏi liên quan
TM
3 tháng 5 2023
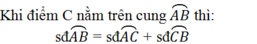
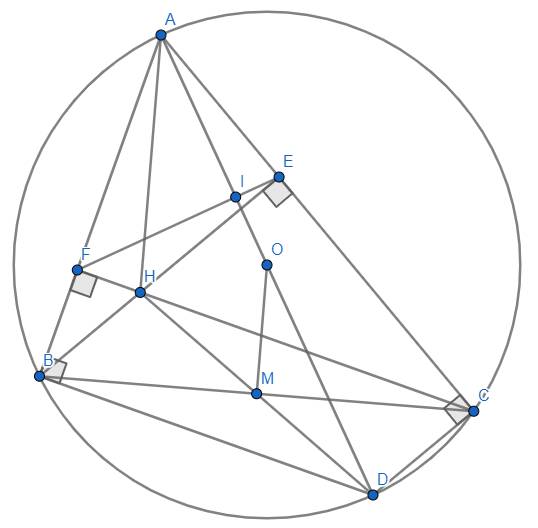
a) \(BE,CF\) là đường cao của \(\Delta ABC\Rightarrow\hat{BFC}=\hat{BEC}=90^o\).
Mà trong tứ giác \(BFEC\), hai góc này có đỉnh kề nhau và cùng nhìn cạnh \(BC\).
Vậy : Tứ giác \(BFEC\) nội tiếp được một đường tròn (dấu hiệu nhận biết) (đpcm).
b) Ta có : \(\hat{ABD}=90^o\) (góc nội tiếp chắn nửa đường tròn) \(\Rightarrow AB\perp BD.\)
Mà : \(\hat{BFC}=90^o\left(cmt\right)\Rightarrow AB\perp CF.\)
Từ đó suy ra : \(BD\left|\right|CF\Rightarrow BFCD\) là hình thang.
Mà : \(\hat{BFC}=\hat{ABD}=90^o\left(cmt\right)\Rightarrow BFCD\) là hình thang vuông.
c) Ta có : \(CF\left|\right|BD\left(cmt\right)\) hay \(CH\left|\right|BD\left(1\right).\)
Mặt khác : \(\hat{ACD}=90^o\) (góc nội tiếp chắn nửa đường tròn) \(\Rightarrow AC\perp CD\).
Và : \(BE\perp AC\left(gt\right)\)
Suy ra được : \(CD\left|\right|BE\) hay \(CD\left|\right|BH\left(2\right).\)
Từ \(\left(1\right),\left(2\right)\Rightarrow BHCD\) là hình bình hành.
Ta cũng có : \(M\) là trung điểm của \(BC\left(gt\right)\Rightarrow M\) cũng là trung điểm của \(HD\left(3\right).\)
Lại có \(O\) là trung điểm của \(AD\left(4\right)\) (tâm đường tròn).
Từ \(\left(3\right),\left(4\right)\Rightarrow OM\) là đường trung bình của \(\Delta HAD\Rightarrow OM=\dfrac{1}{2}AH\Leftrightarrow AH=2.OM\) (đpcm).
d) Cho \(I\) là giao điểm của \(OA\) và \(EF\).
Ta có : \(\hat{ACB}=\hat{ADB}\) (hai góc nội tiếp cùng chắn \(\stackrel\frown{AB}\)).
Hay : \(\hat{ACB}=\hat{BDI}\left(5\right).\)
Mặt khác : Tứ giác \(BFEC\) nội tiếp được một đường tròn (cmt) nên \(\hat{AFI}=\hat{ECB}\) (cùng bù với \(\hat{BFE}\)) hay \(\hat{AFI}=\hat{ACB}\left(6\right).\)
Từ \(\left(5\right),\left(6\right)\Rightarrow\hat{AFI}=\hat{BDI}\) hay \(\hat{AFI}=\hat{ADB}.\)
\(\Delta ABD:\hat{BAD}+\hat{ADB}=90^o\) (hai góc phụ nhau)
\(\Rightarrow\hat{FAI}+\hat{AFI}=90^o.\)
\(\Delta AFI:\hat{FAI}+\hat{AFI}+\hat{AIF}=180^o\) (tổng ba góc trong một tam giác)
\(\Leftrightarrow\hat{AIF}=180^o-\left(\hat{FAI}+\hat{AFI}\right)=180^o-90^o=90^o\)
\(\Rightarrow OA\perp EF\) (đpcm).
SV
21 tháng 3 2015
a) BS, BE là phân giác của hai góc kề bù nên góc SBE =900
tương tự góc SCE = 900 => tứ giác BSCE nội tiếp
b) góc ASB = \(180^0-\left(gocBAS+gocABS\right)\)(tổng 3 góc trog tg ASB)
=> góc ASB = \(180^0-\left(\frac{gócABC}{2}+\frac{gocBAC}{2}\right)=180^0-\frac{gocABC+gocBAC}{2}\)
= \(180^0-\frac{180^0-gocACB}{2}=90^0+\frac{gocACB}{2}\) (1)
Ta lại có : góc BSE = 900 - góc BES mà góc BES = góc BCS( BSCE nội tiếp) ; góc BCS = góc ACB/2 => góc BES = góc ACB/2
=> góc BSE = \(90^0-\frac{gócACB}{2}\)(2)
từ (1) và (2) => góc ASB + góc BSE = 1800. Vậy A, S, E thẳng hàng
28 tháng 1 2021
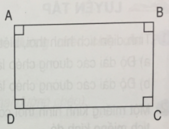
1. AB // CD (ABCD là hình thang) => ^B + ^D = 180o (Trong cùng phía)
Mà ^B = ^A (ABCD là hình thang) => ^A + ^D = 180o
Xét hình thang ABCD có: ^A đối diện với ^D
^A + ^D = 180o (cmt)
=> hình thang ABCD nội tiếp đường tròn
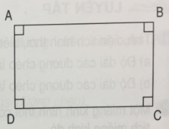
2. Xét hình chữ nhật LMNO có:
^L + ^N = 180o (^L = 90o; ^N = 90o)
=> hình chữ nhật LMNO nội tiếp đường tròn
3. Xét hình vuông PQRS có:
^P + ^R = 180o (^P = 90o; ^R = 90o)
=> hình vuông PQRS nội tiếp đường tròn