Tìm cực trị của các hàm số sau: y = sin2x
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) y = sin2x
Hàm số có chu kỳ T = π
Xét hàm số y=sin2x trên đoạn [0;π], ta có:
y' = 2cos2x
y' = 0 ⇔ 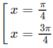
Bảng biến thiên:
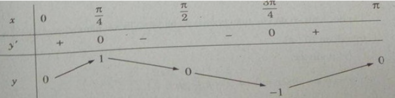
Do đó trên đoạn [0;π] , hàm số đạt cực đại tại π/4 , đạt cực tiểu tại 3π/4 và y C D = y(π/4) = 1; y C T = y(3π/4) = −1
Vậy trên R ta có:
y C Đ = y(π/4 + kπ) = 1;
y C T = y(3π/4 + kπ) = −1, k∈Z
b) Hàm số tuần hoàn chu kỳ nên ta xét trên đoạn [−π;π].
y′ = − sinx – cosx
y′ = 0 ⇔ tanx = −1 ⇔ x = −π4 + kπ, k∈Z
Lập bảng biến thiên trên đoạn [−π;π]
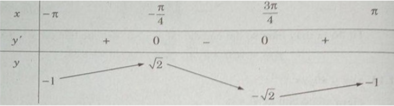
Hàm số đạt cực đại tại x = −π4 + k2π , đạt cực tiểu tại x = 3π4 + k2π (k∈Z) và
y C Đ = y(−π4 + k2π) = 2 ;
y C T = y(3π4 + k2π) = − 2 (k∈Z).
c) Ta có:
![]()
Do đó, hàm số đã cho tuần hoàn với chu kỳ π.
Ta xét hàm số y trên đoạn [0;π]:
![]()
y′ = sin2x
y′ = 0 ⇔ sin2x = 0 ⇔ x = kπ/2 (k∈Z)
Lập bảng biến thiên trên đoạn [0,π]
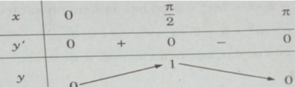
Từ đó, ta thấy hàm số đạt cực tiểu tại x = kπ/2 với k chẵn, đạt cực đại tại x = kπ/2 với k lẻ, và
y C T = y(2mπ) = 0; yCT = y(2mπ) = 0;
y C Đ = y((2m+1)π/2) = 1 (m∈Z)

Ta có:
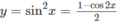
Do đó, hàm số đã cho tuần hoàn với chu kỳ π
Ta xét hàm số y trên đoạn [0; π ]:
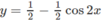
y′ = sin2x
y′ = 0 ⇔ sin2x = 0 ⇔ x = k π /2 (k ∈ Z)
Lập bảng biến thiên trên đoạn [0, π ]
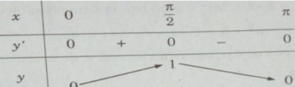
Từ đó, ta thấy hàm số đạt cực tiểu tại x = k π /2 với k chẵn, đạt cực đại tại x = k π /2 với k lẻ, và
y CT = y(2m π ) = 0; y CT = y(2m π ) = 0;
y CD = y((2m+1) π /2) = 1 (m ∈ Z)

TXĐ: D = R
+ y' = 2cos2x – 1;
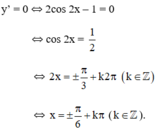
+ y" = -4.sin2x
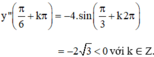
⇒ 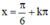 (k ∈ Z) là các điểm cực đại của hàm số.
(k ∈ Z) là các điểm cực đại của hàm số.
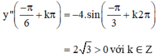
⇒ 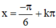 (k ∈ Z) là các điểm cực tiểu của hàm số.
(k ∈ Z) là các điểm cực tiểu của hàm số.

TXĐ: R
y' = 1 - 2cos2x
y' = 0 ⇔x = kπ (k ∈ Z)
y'' = 2sin2x
x = kπ → y'' = 2 > 0
→ yCT = 1 tại x = kπ




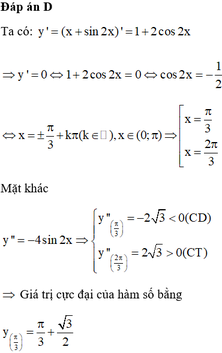
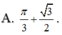
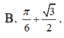
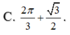
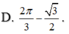
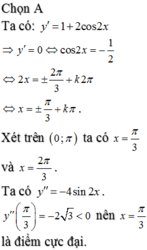
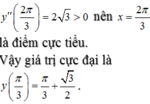
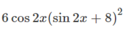
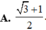
y = sin2x
Hàm số có chu kỳ T = π
Xét hàm số y=sin2x trên đoạn [0; π ], ta có:
y' = 2cos2x
y' = 0 ⇔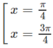
Bảng biến thiên:
Do đó trên đoạn [0; π ] , hàm số đạt cực đại tại π /4 , đạt cực tiểu tại 3 π /4 và y CD = y( π /4) = 1; y CT = y(3 π /4) = −1
Vậy trên R ta có:
y CD = y( π /4 + k π ) = 1;
y CT = y(3 π /4 + k π ) = −1, k ∈ Z