Một người đi xe máy từ địa điểm A đến địa điểm B cách nhau 4,8km. Nửa quãng đường đầu, xe mấy đi với v 1 , nửa quãng đường sau đi với v 2 bằng một phần hai v 1 . Xác định v 1 , v 2 sao cho sau 15 phút xe máy tới địa điểm B
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Giải:
Ta có S 1 = v 1 . t 1 ⇒ t 1 = S 1 v 1 = S 2. v 1 = 4800 2. v 1 = 2400 v 1
S 2 = v 2 . t 2 ⇒ t 2 = S 2 v 2 = S 2. v 1 2 = S v 1 = 4800 v 1
Mặt khác: t 1 + t 2 = 900 ⇒ 2400 v 1 + 4800 v 1 = 900 ⇒ v 1 = 8 m / s ; v 2 = 4 m / s

theo đề bài ta có \(v2=\dfrac{v1}{2}\)
thời gian xe thứ nhất đi được nữa quãng đường đầu
\(t1=\dfrac{s1}{v1}=\dfrac{\dfrac{1}{2}s}{\dfrac{2v1}{2}}=\dfrac{s}{2v1}=\dfrac{4}{2v1}\)
thời gian xe thứ nhất đi được nữa quãng đường sau
\(t2=\dfrac{s2}{v2}=\dfrac{\dfrac{1}{2}s}{\dfrac{1}{2}v1}=\dfrac{s}{v1}=\dfrac{4}{v1}\)
ta có \(t1+t2=t\)
\(\dfrac{4}{2v1}+\dfrac{4}{v1}=\dfrac{1}{6}\)
\(\dfrac{12}{6v1}+\dfrac{24}{6v1}=\dfrac{v1}{6v1}\)
\(v1=\dfrac{36km}{h}\) vậy giả thiết \(v2=\dfrac{v1}{2}=>v2=\dfrac{36}{2}=\dfrac{18km}{h}\)
chỉ cần tìm vtb1 và vtb2 là tính được cả ý dưới
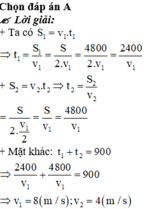
Mặt khác: