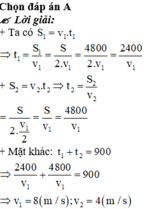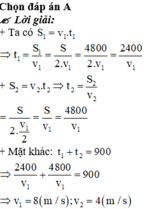c1 vận tốc của 1 chất điểm chuyển động dọc theo trục Ox cho bởi hệ thức v=15-8t (m/s) . Gía trị của gia tốc và tốc độ của chất điểm lúc t=2s là
A 8m/\(s^2\) và -1m/s B 8m/\(S^2\)Và 1m/s C -8m/\(s^2\) và 1m/s D -8m/\(s^2\) và -1m/s
C2 một vật chuyển động thẳng chậm dần đều với tốc độ đầu 3m/s và gia tốc 2m/\(s^2\) , thời điểm ban đầu của gốc toạ độ và chuyển động ngược chiều dương của trục tọa độ thì phương tring=hf có dạng
A x=3t+\(t^2\) B x=-3t-2\(t^2\) C x= -3t+\(t^2\) D x= 3t-\(t^2\)
C3 một chất điểm chuyển động thẳng biến đổi đều có phương trình chuyển động là x=-\(t^2\) +3t+2(x đo bằng m, ; t đo bằng giây) . Công thức tính vận tốc có dạng nào dưới đây?
A v=3+2t B v=2+2t C v=2t D v=3-2t
C4 một ô tô chuyển động chậm dần đều . Sau 10s , vận tốc của ô tô giảm từ 6m/s về 4m/s .Quãng đường ô tô đi được trong khoảng thời gian 10sđó là
A 70m B 50m C 40m D100m
C5 một đoàn tàu chạy với vận tốc 72km/h thì hãm phanh xe chuyển động chậm dần đều sau 5s thì dừng hẳn . Quãng đường mà tàu đi được từ lúc bắt đầu hãm phanh đến lúc dừng lại là
A 4m B 50m C18m D 14,4m
C6 một xe lửa bắt đầu dời khỏi ga và chuyển động thẳng nhanh dần đều với gia tốc 0,1m/\(s^2\) . Khoảng thời gian để xe lửa đạt được vận tốc 36km/h :
A 360s B 100s C 300s D200s
C7 một đoàn tàu đứng yên khi tăng tốc , chuyển động nhanh dần đều . Trong khoảng thời gian tăng tốc từ 21,6km /h đến 36km/h , tàu đi được 64m . Gia tóc của tàu và quãng đường tàu đi được kể từ lúc bắt đầu chuyển động đến khi đạt tốc độ 36km/h là
A a= 0,5m/\(s^2\) , s=100sm B a= -0,5m/s\(s^2\) , s= 110m C a= -0,5m/\(s^2\), s= 100m D a= -0,7m/\(s^2\) , s= 200m
C 8 một xe máy đang chạy với tốc độ 36km/h bỗng người lái xe thấy có 1 cái hố trước mặt cách xe 20 m . Người ấy phanh gấp và xe đế ngay trước miệng hố thì dừng lại . Gia tốc của xe máy là:
A 2,5m/\(s^2\) B -2,5m/\(s^2\) C 5,09m/\(s^2\) D 4,1m/\(s^2\)
C9 một ô tô đang chuyển động thẳng đều với tốc độ 40km/h bỗng tăng tốc và chuyển động nhanh dần đều . Tính gia tốc của xe biết rằng sau khi đi được quãng đường 1km thì ô tô đạt được tốc độ 60km/h
A 0,05m/\(s^2\) B 1m/\(s^2\) C 0,0772m/\(s^2\) D 10m/\(s^2\)
C10 một ô tô đang chuyển động với vận tốc 10m/s thì bắt đầu chuyển động nhanh dần đều . Sau 20s ô tô đạt vận tóc 14m/s. Sau 40s kể từ lúc tăng tốc , gia tốc và vận tốc của ô tô lần lượt là:
A 0,7m/\(s^2\) , 38m/s B 0,2m/\(s^2\) , 8m/s C 1,4m/\(s^2\) , 66m/s D 0,2m/\(s^2\) , 18m/s
C11 hai điểm Avà B cách nhau 200m , tại A có 1 ô tô có vận tốc 3m/s và đang chuyển động nhanh dần đều với gia tốc 2m/\(s^2\) đi đến B . Cùng lúc đó 1 ô tô khác bắt đầu khời hành tư B về A với gia tốc 2,8m/\(s^2\) . Hai xe gặp nhau cách A 1 khảng bằng :
A 85,75 B 98,25m C 105,32m D 115,95m
C12 2 người đi xe đạp khởi hanh cùng 1 lúc và đi ngược chiều nhau . Người thứ nhất có vận tốc đầu là 18km/h và chuyển động thẳng chậm dần đều với gia tốc 20m/\(s^2\) . Người thứ 2 có vận tốc đầu là 5,4km/h và chuyển động nhanh đều với gia tốc 0,2m/\(s^2\) . Khoảng cách giữa 2 người là 130m . Hỏi sau bao lâu 2 người gặp nhau và vi trí gặp nhau
A t=20s , cách A 60m B t =17,5s , cách A 56,9m C t=20m , cách B 60km D t= 17,5s , cách B 56,9m