Chu kì dao động của con lắc đơn là 1s. Thời gian ngắn nhất để con lắc đi từ vị trí mà tại đó động năng cực đại đến vị trí mà tại đó động năng bằng 3 lần thế năng bằng:
A. 1/3 s.
B. 2/13 s.
C. 1/12 s.
D. 2/3 s.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Vận tốc có độ lớn cực đại là 0,4m/s nên ![]()
Lúc vật đang ở vị trí x=2(cm) theo chiều dương thì tại đó động năng bằng ba lần thế năng nên:
W đ = 3 W t ⇒ 4 W t = W ⇒ 4 kx 2 2 = kA 2 2 ⇒ A = 2 x = 4 cm .
Gốc thời gian tại lúc này nên
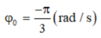
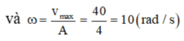
Vậy phương trình dao động của vật là:
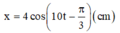

Chọn đáp án B
Vận tốc có độ lớn cực đại là 0 , 4 m / s nên A ω = 0 , 4 m / s = 40 c m / s
Lúc vật đang ở vị trí x = 2 c m theo chiều dương thì tại đó động năng bằng ba lần thế năng nên:
W d = 3 W t ⇒ 4 W t = W ⇒ 4. k x 2 2 = k A 2 2
⇒ A = 2 x = 4 c m
Gốc thời gian tại lúc này nên φ 0 = − π 3 (rad/s) và ω = v max A = 40 4 = 10 r a d / s
Vậy phương trình dao động của vật là: x = 4 cos 10 t − π 3 c m

Đáp án B
Vận tốc có độ lớn cực đại là 0 , 4 m / s nên A ω = 0 , 4 m / s = 40 c m / s
Lúc vật đang ở vị trí x = 2 c m theo chiều dương thì tại đó động năng bằng ba lần thế năng nên:
![]()
Gốc thời gian tại lúc này nên φ 0 = - π 3 r a d / s và ω = v m a x A = 40 4 = 10 r a d / s
Vậy phương trình dao động của vật là: 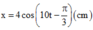

Đáp án B
Vận tốc có độ lớn cực đại là 0,4m/s nên A ω = 0 , 4 m / s = 40 c m / s
Lúc vật đang ở vị trí x = 2 c m theo chiều dương thì tại đó động năng bằng ba lần thế năng nên: W d = 3 W t ⇒ 4 W t = W ⇒ 4 ⋅ k x 2 2 = k A 2 2 ⇒ A = 2 x = 4 c m
Gốc thời gian tại lúc này nên φ 0 = − π 3 r a d / s và ω = v max A = 40 4 = 10 r a d / s
Vậy phương trình dao động của vật là: x = 4 cos 10 t − π 3 c m

+ Ta có: F k m a x = m g a 0 = 0 , 05 → a 0 = 0 , 1 r a d
+ W t = 1 2 W d ® W = 3 W t = 3 m g l ( 1 - cos a )
+ Áp dụng bảo toàn cơ năng ta được: 3 m g l ( 1 - cos a ) = m g l ( 1 - cos a 0 )
® cos α = 2 + c os α 0 3
+ T = m g ( 3 cos a - 2 cos a 0 ) = 0 , 5025 N
Đáp án B

1/ Bước sóng: \(\lambda=v/f=0,2m\)
Ta có: \(2.[\dfrac{AB}{\lambda}+0,5]=2.[\dfrac{1,1}{0,2}+0,5]=12\)
Do \(\dfrac{1,1}{0,2}+0,5=6\) là giá trị nguyên, mà ở 2 đầu A, B không có cực đại cực tiểu, nên số điểm không dao động trên đoạn AB là: \(12-2=10\)
Chọn C.

Với con lắc đơn, ta có hệ số hồi phục \(k=\frac{mg}{l}\)
Lực hồi phục: \(F_{hp}=-kx\)
Với x là li độ dài, \(x=\alpha l\)
Suy ra: \(F_{hp}=-\frac{mg}{l}.\alpha l=-mg\alpha\) \(\Rightarrow F_{hpmax}=mg\alpha_0\) \(\Rightarrow\alpha_0=\frac{F_{hpmax}}{mg}=\frac{0,1}{0,1.10}=0,1rad\)(1)
Lực căng dây: \(\tau=mg\left(3\cos\alpha-2\cos\alpha_0\right)=mg\left(3\left(1-2\sin^2\frac{\alpha}{2}\right)-2\left(1-2\sin^2\frac{\alpha_0}{2}\right)\right)=mg\left(1+\alpha_0^2-\frac{3}{2}\alpha^2\right)\)(do góc \(\alpha\) rất nhỏ nên ta lấy gần đúng)
Tại vị trí \(W_t=\frac{1}{2}W_đ\Leftrightarrow W=3W_t\Leftrightarrow\alpha_0^2=3\alpha^2\Leftrightarrow\alpha=\frac{\alpha_0}{\sqrt{3}}\)
Như vậy, lực căng dây tại vị trí này là: \(\tau=mg\left(1+\alpha_0^2-\frac{3}{2}\alpha^2\right)=mg\left(1+\alpha_0^2-\frac{3}{2}\frac{\alpha_0^2}{3}\right)=mg\left(1+\frac{\alpha_0^2}{2}\right)\)
Thay từ (1) vào ta đc: \(\tau=0,1.10\left(1+\frac{0,1^2}{2}\right)=1,005N\)
Chọn C
+ Động năng cực đại: x=0
+ Động năng bằng 3 lần thế năng
=> 4 W t = W ⇒ 4 . k x 2 2 = k A 2 2 ⇒ x = ± A 2
+ Thời gian ngắn nhất để con lắc đi như đề ra:
t = T 12 = 1 12 s .