Giải bất phương trình f ' ( x ) < g ' ( x ) , với f ( x ) = x 3 + x 2 − 1 2 ; g ( x ) = 2 3 x 3 + 1 2 x 2 + 2 x
A. S = (1; 2)
B. S= (-2; 1)
C. S = ( -1; 2)
D. S= (-2; -1)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(a,f'\left(x\right)=3x^2-6x\\ f'\left(x\right)\le0\Leftrightarrow3x^2-6x\le0\\ \Leftrightarrow3x\left(x-2\right)\le0\Leftrightarrow0\le x\le2\)
Lời giải:
a. $f'(x)\leq 0$
$\Leftrightarrow 3x^2-6x\leq 0$
$\Leftrightarrow x(x-2)\leq 0$
$\Leftrightarrow 0\leq x\leq 2$
b.
$f'(x)=x^2-3x+2=0$
$\Leftrightarrow 3x^2-6x=x^2-3x+2=0$
$\Leftrightarrow 3x(x-2)=(x-1)(x-2)=0$
$\Leftrightarrow x-2=0$
$\Leftrightarrow x=2$
c.
$g(x)=f(1-2x)+x^2-x+2022$
$g'(x)=(1-2x)'f(1-2x)'_{1-2x}+2x-1$
$=-2[3(1-2x)^2-6(1-2x)]+2x-1$
$=-24x^2+2x+5$
$g'(x)\geq 0$
$\Leftrightarrow -24x^2+2x+5\geq 0$
$\Leftrightarrow (5-12x)(2x-1)\geq 0$
$\Leftrightarrow \frac{-5}{12}\leq x\leq \frac{1}{2}$

Đáp án B
Ta có:
f ' x = 2 x 3 + x − 2 / = 6 x 2 + 1
g ' x = 3 x 2 + x + 2 / = 6 x + 1
f ' x > g ' x ⇔ 6 x 2 + 1 > 6 x + 1 ⇔ 6 x 2 − 6 x > 0 ⇔ x ∈ − ∞ ; 0 ∪ 1 ; + ∞

Vẽ đồ thị:
- Vẽ đồ thị hàm số y = f(x) = x + 1 qua hai điểm (0; 1) và (-1; 0).
- Vẽ đồ thị hàm số y = g(x) = 3 - x qua hai điểm (0; 3) và (3; 0)
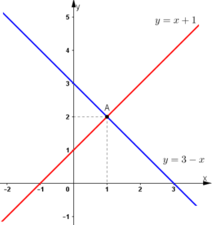
a) Nghiệm của phương trình f(x) = g(x) chính là hoành độ giao điểm của hai đường thẳng y = f(x) và y = g(x).
Giao điểm của hai đường thẳng y = x + 1 và y = 3 – x là điểm A(1; 2).
Do đó phương trình f(x) = g(x) có nghiệm x = 1.
Kiểm tra bằng tính toán:
f(x) = g(x) ⇔ x + 1 = 3 - x ⇔ 2x = 2 ⇔ x = 1.
b) Khi x > 1 thì đồ thị hàm số y = f(x) nằm phía trên đồ thị hàm số y = g(x), hay với x > 1 thì f(x) > g(x).
Kiểm tra bằng tính toán:
f(x) > g(x) ⇔ x + 1 > 3 - x ⇔ 2x > 2 ⇔ x > 1.
c) Khi x < 1 thì đồ thị hàm số y = f(x) nằm phía dưới đồ thị hàm số y = g(x), hay với x < 1 thì f(x) < g(x).
Kiểm tra bằng tính toán:
f(x) < g(x) ⇔ x + 1 < 3 - x ⇔ 2x < 2 ⇔ x < 1.

2: ĐKXĐ: x<>1
\(f'\left(x\right)=\dfrac{\left(x^2-3x+3\right)'\left(x-1\right)-\left(x^2-3x+3\right)\left(x-1\right)'}{\left(x-1\right)^2}\)
\(=\dfrac{\left(2x-3\right)\left(x-1\right)-\left(x^2-3x+3\right)}{\left(x-1\right)^2}\)
\(=\dfrac{2x^2-5x+3-x^2+3x-3}{\left(x-1\right)^2}=\dfrac{x^2-2x}{\left(x-1\right)^2}\)
f'(x)=0
=>x^2-2x=0
=>x(x-2)=0
=>\(\left[{}\begin{matrix}x=0\\x=2\end{matrix}\right.\)
1:
\(f\left(x\right)=\dfrac{1}{3}x^3-2\sqrt{2}\cdot x^2+8x-1\)
=>\(f'\left(x\right)=\dfrac{1}{3}\cdot3x^2-2\sqrt{2}\cdot2x+8=x^2-4\sqrt{2}\cdot x+8=\left(x-2\sqrt{2}\right)^2\)
f'(x)=0
=>\(\left(x-2\sqrt{2}\right)^2=0\)
=>\(x-2\sqrt{2}=0\)
=>\(x=2\sqrt{2}\)
Ta có f ' ( x ) = 3 x 2 + 2 x , g ' ( x ) = 2 x 2 + x + 2
f ' ( x ) < g ' ( x ) ⇔ 3 x 2 + 2 x < 2 x 2 + x + 2 ⇔ 3 x 2 + 2 x − 2 x 2 − x − 2 < 0 ⇔ x 2 + x − 2 < 0 ⇔ − 2 < x < 1
Vậy tập nghiệm bất phương trình là: S=(-2 ; 1).
Chọn đáp án B