Giải bất phương trình với
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(a,f'\left(x\right)=3x^2-6x\\ f'\left(x\right)\le0\Leftrightarrow3x^2-6x\le0\\ \Leftrightarrow3x\left(x-2\right)\le0\Leftrightarrow0\le x\le2\)
Lời giải:
a. $f'(x)\leq 0$
$\Leftrightarrow 3x^2-6x\leq 0$
$\Leftrightarrow x(x-2)\leq 0$
$\Leftrightarrow 0\leq x\leq 2$
b.
$f'(x)=x^2-3x+2=0$
$\Leftrightarrow 3x^2-6x=x^2-3x+2=0$
$\Leftrightarrow 3x(x-2)=(x-1)(x-2)=0$
$\Leftrightarrow x-2=0$
$\Leftrightarrow x=2$
c.
$g(x)=f(1-2x)+x^2-x+2022$
$g'(x)=(1-2x)'f(1-2x)'_{1-2x}+2x-1$
$=-2[3(1-2x)^2-6(1-2x)]+2x-1$
$=-24x^2+2x+5$
$g'(x)\geq 0$
$\Leftrightarrow -24x^2+2x+5\geq 0$
$\Leftrightarrow (5-12x)(2x-1)\geq 0$
$\Leftrightarrow \frac{-5}{12}\leq x\leq \frac{1}{2}$

1
a (9+x)=2 ta có (9+x)= 9+x khi 9+x >_0 hoặc >_ -9
(9+x)= -9-x khi 9+x <0 hoặc x <-9
1)pt 9+x=2 với x >_ -9
<=> x = 2-9
<=> x=-7 thỏa mãn điều kiện (TMDK)
2) pt -9-x=2 với x<-9
<=> -x=2+9
<=> -x=11
x= -11 TMDK
vậy pt có tập nghiệm S={-7;-9}
các cau con lai tu lam riêng nhung cau nhan với số âm thi phan điều kiện đổi chiều nha vd
nhu cau o trên mk lam 9+x>_0 hoặc x>_0
với số âm thi -2x>_0 hoặc x <_ 0 nha

a) \(2{x^2} + 3x + 1 \ge 0\)
Tam thức bậc hai \(f\left( x \right) = 2{x^2} + 3x + 1\) có 2 nghiệm phân biệt \(x = - 1,x = \frac{{ - 1}}{2}\)
hệ số \(a = 2 > 0\)
Ta có bảng xét dấu f(x) như sau:
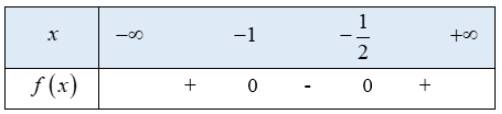
Từ bảng xét dấu ta thấy \(f\left( x \right) \ge 0 \Leftrightarrow \left[ \begin{array}{l}x \le - 1\\x \ge - \frac{1}{2}\end{array} \right.\)
Vậy tập nghiệm của bất phương trình là \(\left( { - \infty ; - 1} \right] \cup \left[ { - \frac{1}{2}; + \infty } \right)\)
b) \( - 3{x^2} + x + 1 > 0\)
Tam thức bậc hai \(f\left( x \right) = - 3{x^2} + x + 1\) có 2 nghiệm phân biệt \(x = \frac{{1 - \sqrt {13} }}{6},x = \frac{{1 + \sqrt {13} }}{6}\)
Hệ số \(a = - 3 < 0\)
Ta có bảng xét dấu f(x) như sau:

Từ bảng xét dấu ta thấy \(f\left( x \right) > 0\)\( \Leftrightarrow \frac{{1 - \sqrt {13} }}{6} < x < \frac{{1 + \sqrt {13} }}{6}\)
Vậy tập nghiệm của bất phương trình là \(\left( {\frac{{1 - \sqrt {13} }}{6};\frac{{1 + \sqrt {13} }}{6}} \right)\)
c) \(4{x^2} + 4x + 1 \ge 0\)
Tam thức bậc hai \(f\left( x \right) = 4{x^2} + 4x + 1\) có nghiệm duy nhất \(x = \frac{{ - 1}}{2}\)
hệ số \(a = 4 > 0\)
Ta có bảng xét dấu f(x) như sau:

Từ bảng xét dấu ta thấy \(f\left( x \right) \ge 0 \Leftrightarrow x \in \mathbb{R}\)
Vậy tập nghiệm của bất phương trình là \(\mathbb{R}\)
d) \( - 16{x^2} + 8x - 1 < 0\)
Tam thức bậc hai \(f\left( x \right) = - 16{x^2} + 8x - 1\) có nghiệm duy nhất \(x = \frac{1}{4}\)
hệ số \(a = - 16 < 0\)
Ta có bảng xét dấu f(x) như sau:
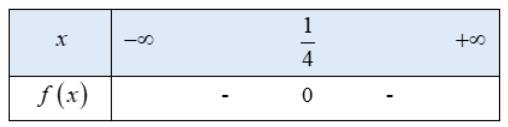
Từ bảng xét dấu ta thấy \(f\left( x \right) < 0 \Leftrightarrow x \ne \frac{1}{4}\)
Vậy tập nghiệm của bất phương trình là \(\mathbb{R}\backslash \left\{ {\frac{1}{4}} \right\}\)
e) \(2{x^2} + x + 3 < 0\)
Ta có \(\Delta = {1^2} - 4.2.3 = - 23 < 0\) và có \(a = 2 > 0\)
Sử dụng định lí về dấu của tam thức bậc hai, ta thấy tập hợp những giá trị của x sao cho \(2{x^2} + x + 3\) mang dấu “-” là \(\emptyset \)
Vậy tập nghiệm của bất phương trình \(2{x^2} + x + 3 < 0\) là \(\emptyset \)
g) \( - 3{x^2} + 4x - 5 < 0\)
Tam thức bậc hai \(f\left( x \right) = - 3{x^2} + 4x - 5\) có \(\Delta ' = {2^2} - \left( { - 3} \right).\left( { - 5} \right) = - 11 < 0\) và có \(a = - 3 < 0\)
Sử dụng định lí về dấu của tam thức bậc hai, ta thấy tập hợp những giá trị của x sao cho \( - 3{x^2} + 4x - 5\) mang dấu “-” là \(\mathbb{R}\)
Vậy tập nghiệm của bất phương trình \( - 3{x^2} + 4x - 5 < 0\) là \(\mathbb{R}\)

Bất phương trình bậc nhất 2 ẩn :
\(2x+3y>0\Rightarrow Câu\) \(C\)
\(x-2y\le1\Rightarrow Câu\) \(f\)
\(4\left(x-1\right)+5\left(y-3\right)>2x-9\)
\(\Leftrightarrow4x-4+5y-15-2x+9>0\)
\(\Leftrightarrow2x+5y-10>0\) \(\Rightarrow Câu\) \(i\)

hoc gioi the hihiihihihhhihihihihiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiii
,mnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnn

a, \(16x^2-5=0\)
\(\Rightarrow16x^2=5\)
\(\Rightarrow x^2=\frac{5}{16}\)
\(\Rightarrow x=\sqrt{\frac{5}{16}}\Rightarrow x=\frac{\sqrt{5}}{4}\)
b, \(2\sqrt{x-3}=4\)
\(\Rightarrow\sqrt{x-3}=4:2\)
\(\Rightarrow\sqrt{x-3}=2\)
\(\Rightarrow x-3=4\)
\(\Rightarrow x=4+3\)
\(\Rightarrow x=7\)
c, \(\sqrt{4x^2-4x+1}=3\)
\(\Rightarrow\sqrt{\left(2x-1\right)^2}=3\)
\(\Rightarrow2x-1=3\)
\(\Rightarrow2x=4\)
\(\Rightarrow x=2\)
d, \(\sqrt{x+3}\ge5\)
\(\Rightarrow x+3\ge25\)
\(\Rightarrow x\ge22\)
e, \(\sqrt{3x-1}< 2\)
\(\Rightarrow3x-1< 4\)
\(\Rightarrow3x< 5\)
\(\Rightarrow x< \frac{5}{3}\)
g, \(\sqrt{x^2-9}+\sqrt{x^2-6x+9}=0\)
\(\Rightarrow\sqrt{\left(x-3\right)\left(x+3\right)}+\sqrt{\left(x-3\right)^2}=0\)
\(\Rightarrow\sqrt{x-3}\left(\sqrt{x+3}+\sqrt{x-3}\right)=0\)
\(\left(\sqrt{x+3}+\sqrt{x-3}\right)>0\)
\(\Rightarrow\sqrt{x-3}=0\)
\(\Rightarrow x-3=0\)
\(\Rightarrow x=3\)
a) \(16x^2-5=0\)
\(\Leftrightarrow16x^2=5\)
\(\Leftrightarrow x^2=\frac{5}{16}\)
\(\Leftrightarrow x=\pm\sqrt{\frac{5}{16}}\)
b) \(2\sqrt{x-3}=4\)
\(\Leftrightarrow\sqrt{x-3}=2\)
\(\Leftrightarrow x-3=4\)
\(\Leftrightarrow x=7\)
c) \(\sqrt{4x^2-4x+1}=3\)
\(\Leftrightarrow\sqrt{\left(2x-1\right)^2}=3\)
\(\Leftrightarrow2x-1=3\)
\(\Leftrightarrow2x=4\)
\(\Leftrightarrow x=2\)
d) \(\sqrt{x+3}\ge5\)
\(\Leftrightarrow x+3\ge25\)
\(\Leftrightarrow x\ge22\)
e) \(\sqrt{3x-1}< 2\)
\(\Leftrightarrow3x-1< 4\)
\(\Leftrightarrow3x< 5\)
\(\Leftrightarrow x< \frac{5}{3}\)
g) \(\sqrt{x^2-9}+\sqrt{x^2-6x+9}=0\)
\(\Leftrightarrow\sqrt{\left(x-3\right)\left(x+3\right)}+\sqrt{\left(x-3\right)^2}=0\)
\(\Leftrightarrow\sqrt{x-3}\left(\sqrt{x+3}+\sqrt{x-3}\right)=0\)
Vì \(\left(\sqrt{x+3}+\sqrt{x-3}\right)>0\)
\(\Leftrightarrow\sqrt{x-3}=0\)
\(\Leftrightarrow x-3=0\)
\(\Leftrightarrow x=3\)
Ta có
g ' ( x ) = ( 2 x + 3 ) . ( x − 2 ) − 1. ( x 2 + 3 x − 9 ) ( x − 2 ) 2 = x 2 − 4 x + 3 ( x − 2 ) 2
Mà g ' ( x ) ≤ 0
⇔ x 2 − 4 x + 3 ≤ 0 x − 2 ≠ 0 ⇔ 1 ≤ x ≤ 3 x ≠ 2 ⇔ x ∈ 1 ; 3 \ 2
Vậy tập nghiệm bất phương trình là: S=[1 ; 3]\{2}
Chọn đáp án B