Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(a,f'\left(x\right)=3x^2-6x\\ f'\left(x\right)\le0\Leftrightarrow3x^2-6x\le0\\ \Leftrightarrow3x\left(x-2\right)\le0\Leftrightarrow0\le x\le2\)
Lời giải:
a. $f'(x)\leq 0$
$\Leftrightarrow 3x^2-6x\leq 0$
$\Leftrightarrow x(x-2)\leq 0$
$\Leftrightarrow 0\leq x\leq 2$
b.
$f'(x)=x^2-3x+2=0$
$\Leftrightarrow 3x^2-6x=x^2-3x+2=0$
$\Leftrightarrow 3x(x-2)=(x-1)(x-2)=0$
$\Leftrightarrow x-2=0$
$\Leftrightarrow x=2$
c.
$g(x)=f(1-2x)+x^2-x+2022$
$g'(x)=(1-2x)'f(1-2x)'_{1-2x}+2x-1$
$=-2[3(1-2x)^2-6(1-2x)]+2x-1$
$=-24x^2+2x+5$
$g'(x)\geq 0$
$\Leftrightarrow -24x^2+2x+5\geq 0$
$\Leftrightarrow (5-12x)(2x-1)\geq 0$
$\Leftrightarrow \frac{-5}{12}\leq x\leq \frac{1}{2}$

\(\begin{array}{l}a)\;\,cos(x + \frac{\pi }{3}) = \frac{{\sqrt 3 }}{2}\\ \Leftrightarrow cos\left( {x + \frac{\pi }{3}} \right) = cos\frac{\pi }{6}\\ \Leftrightarrow \left[ \begin{array}{l}x + \frac{\pi }{3} = \frac{\pi }{6} + k2\pi \\x + \frac{\pi }{3} = -\frac{\pi }{6} + k2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = -\frac{\pi }{6} + k2\pi \\x = -\frac{\pi }{2} + k2\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right)\end{array}\)
\(\begin{array}{l}b)\;\,cos4x = cos\frac{{5\pi }}{{12}}\\ \Leftrightarrow \left[ \begin{array}{l}4x = \frac{{5\pi }}{{12}} + k2\pi \\4x = -\frac{{5\pi }}{{12}} + k2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = \frac{{5\pi }}{{48}} + k\frac{\pi }{2}\\x = -\frac{{5\pi }}{{48}} + k\frac{\pi }{2}\end{array} \right.\left( {k \in \mathbb{Z}} \right)\end{array}\)
\(\begin{array}{l}c)\;\,co{s^2}x = 1\\ \Leftrightarrow \left[ \begin{array}{l}cosx = 1\\cosx = -1\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = k2\pi \\x = \pi + k2\pi \end{array} \right. \Leftrightarrow x = k\pi ,k \in \mathbb{Z}\end{array}\)

a: \(P=-3x^3+5x\)
\(=x\cdot\left(-3x^2\right)+x\cdot5\)
\(=x\left(-3x^2+5\right)\)
b: \(Q=\left(2x-1\right)+\left(x-2\right)\left(2x-1\right)\)
\(=\left(2x-1\right)\left(1+x-2\right)\)
\(=\left(2x-1\right)\left(x-1\right)\)
c: \(R=4-16x^2\)
\(=4\cdot1-4\cdot4x^2\)
\(=4\left(1-4x^2\right)\)
\(=4\left(1-2x\right)\left(1+2x\right)\)
d: \(S=36-4x^2\)
\(=4\cdot9-4\cdot x^2\)
\(=4\left(9-x^2\right)\)
\(=4\left(3-x\right)\left(3+x\right)\)
e: \(T=8x^3-1\)
\(=\left(2x\right)^3-1^3\)
\(=\left(2x-1\right)\left(4x^2+2x+1\right)\)
f: \(Q=8-x^3\)
\(=2^3-x^3\)
\(=\left(2-x\right)\left(4+2x+x^2\right)\)
g: \(N=64-x^3\)
\(=4^3-x^3\)
\(=\left(4-x\right)\left(16+4x+x^2\right)\)

a:
ĐKXĐ: \(x\notin\left\{\dfrac{3}{2};1\right\}\)
\(y=\dfrac{\left(x-2\right)^2}{\left(2x-3\right)\left(x-1\right)}=\dfrac{x^2-4x+4}{2x^2-2x-3x+3}\)
=>\(y=\dfrac{x^2-4x+4}{2x^2-5x+3}\)
=>\(y'=\dfrac{\left(x^2-4x+4\right)'\left(2x^2-5x+3\right)-\left(x^2-4x+4\right)\left(2x^2-5x+3\right)'}{\left(2x^2-5x+3\right)^2}\)
=>\(y'=\dfrac{\left(2x-4\right)\left(2x^2-5x+3\right)-\left(2x-5\right)\left(x^2-4x+4\right)}{\left(2x^2-5x+3\right)^2}\)
=>\(y'=\dfrac{4x^3-10x^2+6x-8x^2+20x-12-2x^3+8x^2-8x+5x^2-20x+20}{\left(2x^2-5x+3\right)^2}\)
=>\(y'=\dfrac{2x^3-5x^2-2x+8}{\left(2x^2-5x+3\right)^2}\)
b:
ĐKXĐ: x<>-3
\(y=\left(x+3\right)+\dfrac{4}{x+3}\)
=>\(y'=\left(x+3+\dfrac{4}{x+3}\right)'=1+\left(\dfrac{4}{x+3}\right)'\)
\(=1+\dfrac{4'\left(x+3\right)-4\left(x+3\right)'}{\left(x+3\right)^2}\)
=>\(y'=1+\dfrac{-4}{\left(x+3\right)^2}=\dfrac{\left(x+3\right)^2-4}{\left(x+3\right)^2}\)
y'=0
=>\(\left(x+3\right)^2-4=0\)
=>\(\left(x+3+2\right)\left(x+3-2\right)=0\)
=>(x+5)(x+1)=0
=>x=-5 hoặc x=-1
c:
ĐKXĐ: x<>-2
\(y=\dfrac{\left(5x-1\right)\left(x+1\right)}{x+2}\)
=>\(y=\dfrac{5x^2+5x-x-1}{x+2}=\dfrac{5x^2+4x-1}{x+2}\)
=>\(y'=\dfrac{\left(5x^2+4x-1\right)'\left(x+2\right)-\left(5x^2+4x-1\right)\left(x+2\right)'}{\left(x+2\right)^2}\)
=>\(y'=\dfrac{\left(5x+4\right)\left(x+2\right)-\left(5x^2+4x-1\right)}{\left(x+2\right)^2}\)
=>\(y'=\dfrac{5x^2+10x+4x+8-5x^2-4x+1}{\left(x+2\right)^2}\)
=>\(y'=\dfrac{10x+9}{\left(x+2\right)^2}\)
\(y'\left(-1\right)=\dfrac{10\cdot\left(-1\right)+9}{\left(-1+2\right)^2}=\dfrac{-1}{1}=-1\)
d:
ĐKXĐ: x<>2
\(y=x-2+\dfrac{9}{x-2}\)
=>\(y'=\left(x-2+\dfrac{9}{x-2}\right)'=1+\left(\dfrac{9}{x-2}\right)'\)
\(=1+\dfrac{9'\left(x-2\right)-9\left(x-2\right)'}{\left(x-2\right)^2}\)
=>\(y'=1+\dfrac{-9}{\left(x-2\right)^2}=\dfrac{\left(x-2\right)^2-9}{\left(x-2\right)^2}\)
y'=0
=>\(\dfrac{\left(x-2\right)^2-9}{\left(x-2\right)^2}=0\)
=>\(\left(x-2\right)^2-9=0\)
=>(x-2-3)(x-2+3)=0
=>(x-5)(x+1)=0
=>x=5 hoặc x=-1

Ta có: \(f'\left(x\right)=x^2-2x-3\)
\(f'\left(x\right)\le0\\ \Rightarrow x^2-2x-3\le0\\ \Leftrightarrow\left(x+1\right)\left(x-3\right)\le0\\ \Leftrightarrow-1\le x\le3\)

a: \(27^{2-x}< =9\)
=>\(\left(3^3\right)^{2-x}< =3^2\)
=>\(3^{6-3x}< =3^2\)
=>6-3x<=2
=>-3x<=-4
=>\(x>=\dfrac{4}{3}\)
b: \(7^{3-x}< 49\)
=>\(7^{3-x}< 7^2\)
=>3-x<2
=>-x<2-3=-1
=>x>1
c: \(27^{3-x}>9\)
=>\(\left(3^3\right)^{3-x}>3^2\)
=>\(3^{9-3x}>3^2\)
=>9-3x>2
=>-3x>-7
=>\(x< \dfrac{7}{3}\)
d: \(2^{3-x}< 2^3\)
=>3-x<3
=>-x<0
=>x>0
e: \(27^{3-x^2}< 27^{x+1}\)
=>\(3-x^2< x+1\)
=>\(-x^2-x+2< 0\)
=>\(x^2+x-2>0\)
=>(x+2)(x-1)>0
=>\(\left[{}\begin{matrix}x>1\\x< -2\end{matrix}\right.\)

Ta có:
\(f'\left(x\right)=6x^2-2x\\ g'\left(x\right)=3x^2+x\)
Theo đề bài, ta có:
\(f'\left(x\right)>g'\left(x\right)\\ \Leftrightarrow6x^2-2x>3x^2+x\\ \Leftrightarrow3x^2-3x>0\\ \Leftrightarrow3x\left(x-1\right)>0\\ \Leftrightarrow\left[{}\begin{matrix}x>1\\x< 0\end{matrix}\right.\)
Vậy tập nghiệm của bất phương trình là \(\left(-\infty;0\right)\cup\left(1;+\infty\right)\)
Chọn D.

\(a,3^{x-1}=27\\ \Leftrightarrow3^{x-1}=3^3\\ \Leftrightarrow x-1=3\\ \Leftrightarrow x=4\\ b,100^{2x^2-3}=0,1^{2x^2-18}\\ \Leftrightarrow10^{4x^2-6}=10^{-2x^2+18}\\ \Leftrightarrow4x^2-6=-2x^2+18\\ \Leftrightarrow6x^2=24\\ \Leftrightarrow x^2=4\\ \Leftrightarrow x=\pm2\)
\(c,\sqrt{3}e^{3x}=1\\ \Leftrightarrow e^{3x}=\dfrac{1}{\sqrt{3}}\\ \Leftrightarrow3x=ln\left(\dfrac{1}{\sqrt{3}}\right)\\ \Leftrightarrow x=\dfrac{1}{3}ln\left(\dfrac{1}{\sqrt{3}}\right)\)
\(d,5^x=3^{2x-1}\\ \Leftrightarrow2x-1=log_35^x\\ \Leftrightarrow2x-1-xlog_35=0\\ \Leftrightarrow x\left(2-log_35\right)=1\\ \Leftrightarrow x=\dfrac{1}{2-log_35}\)

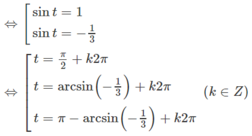
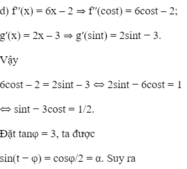
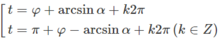
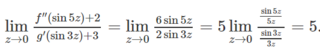
Ta có
g ' ( x ) = ( 2 x + 3 ) . ( x − 2 ) − 1. ( x 2 + 3 x − 9 ) ( x − 2 ) 2 = x 2 − 4 x + 3 ( x − 2 ) 2
Mà g ' ( x ) ≤ 0
⇔ x 2 − 4 x + 3 ≤ 0 x − 2 ≠ 0 ⇔ 1 ≤ x ≤ 3 x ≠ 2 ⇔ x ∈ 1 ; 3 \ 2
Vậy tập nghiệm bất phương trình là: S=[1 ; 3]\{2}
Chọn đáp án B