Cho hàm số y = x + 1 x - 1 M và N là hai điểm thuộc đồ thị hàm số sao cho tiếp tuyến của đồ thị hàm số tại M và N song song với nhau. Khẳng định nào sau đây là SAI?
A. Hai điểm M và N đối xứng nhau qua gốc tọa độ.
B. Đường tiệm cận ngang của đồ thị hàm số đi qua trung điểm của đoạn thẳng MN.
C. Hai điểm M và N đối xứng nhau qua giao điểm của hai đường tiệm cận.
D. Đường tiệm cận đứng của đồ thị hàm số đi qua trung điểm của đoạn thẳng MN.


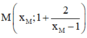
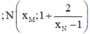
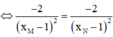
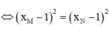
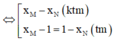
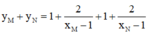
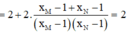

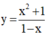
 ]
]
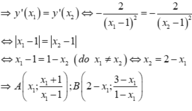
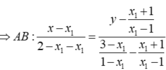
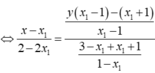
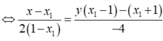
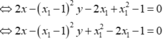


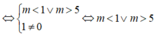
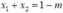 ).
).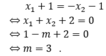
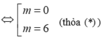


Tiếp tuyến của đồ thị hàm số tại M và N song song với nhau nên hệ số góc của chúng bằng nhau g=hay y ' ( x M ) = y ' ( x N )
y = x + 1 x - 1 = 1 + 2 x - 1 ( x ≠ 1 ) ⇒ y ' = - 2 ( x - 1 ) 2
Gọi M ( x M ; 1 + 2 x M - 1 ) ; M ( x N ; 1 + 2 x N - 1 ) là hai điểm thuộc đồ thị hàm số.
Tiếp tuyến của đồ thị hàm số tại M và N song song với nhau
Gọi I là trung điểm của MN ta có: I (1; 1)
Dễ thấy đồ thị hàm số có TCN là y= 1và tiệm cận đứng x= 1 nên I (1; 1) là giao điểm của hai đường tiệm cận => C đúng.
TCN y= 1 và tiệm cận đứng x= 1 rõ ràng đi qua trung điểm I của đoạn MN=> B, D đúng.
Chọn A.