Với giá trị nào của m, đồ thị hàm số y = x + 1 - x 2 + 3 x x 2 + ( m + 1 ) x - m - 2 có đúng hai đường tiệm cận?
A. m ≤ - 2 m ≠ - 3
B. 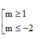
C. mọi m
D. 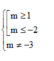
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Để hai đường thẳng song song thì m-1=3-m
=>2m=4
hay m=2
\(\text{//}\Leftrightarrow m-1=3-m\Leftrightarrow m=2\\ \cap\Leftrightarrow m-1\ne3-m\Leftrightarrow m\ne2\)

\(a,\Leftrightarrow3m-1=m+3\Leftrightarrow2m=4\Leftrightarrow m=2\\ b,\Leftrightarrow3m-1\ne m+3\Leftrightarrow m\ne2\)



h: Khi m=3 thì \(y=\left(3-2\right)x+3+1=x+4\)
Gọi \(\alpha\) là góc tạo bởi đồ thị hàm số y=x+4 với trục Ox
\(tan\alpha=a=1\)
=>\(\alpha=45^0\)
y=x+4
=>x-y+4=0
Khoảng cách từ O(0;0) đến đường thẳng x-y+4=0 là:
\(\dfrac{\left|0\cdot1+0\cdot\left(-1\right)+4\right|}{\sqrt{1^2+\left(-1\right)^2}}=\dfrac{4}{\sqrt{2}}=2\sqrt{2}\)

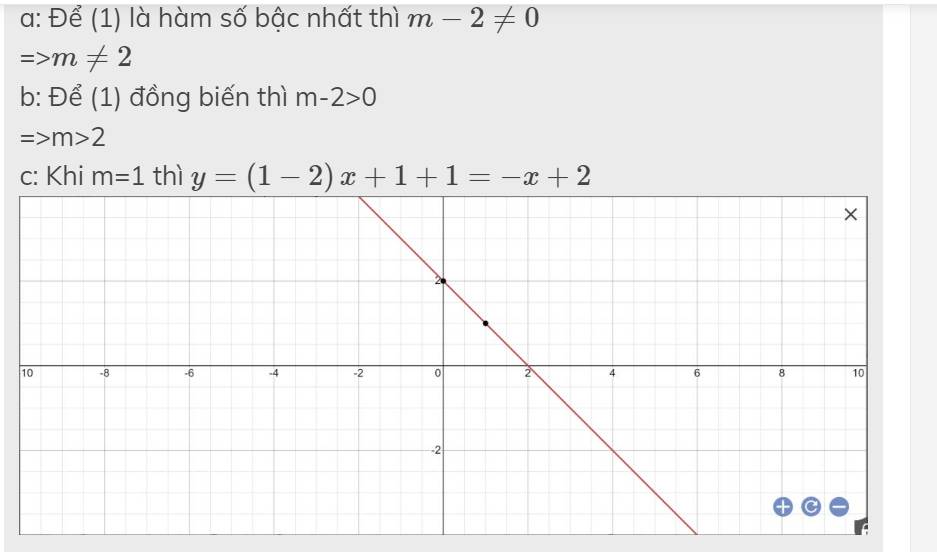
a: Để (1) là hàm số bậc nhất thì \(m-2\ne0\)
=>\(m\ne2\)
b: Để (1) đồng biến thì m-2>0
=>m>2
c: Khi m=1 thì \(y=\left(1-2\right)x+1+1=-x+2\)
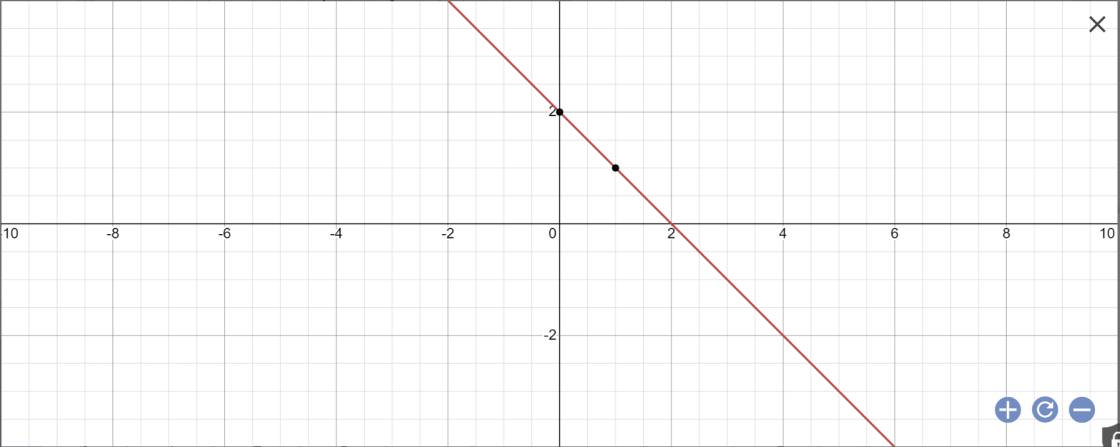
d: Thay x=2 và y=1 vào (1), ta được:
\(2\left(m-2\right)+m+1=1\)
=>2m-4+m=0
=>3m-4=0
=>3m=4
=>\(m=\dfrac{4}{3}\)
e: Để (1)//y=3x+2 thì \(\left\{{}\begin{matrix}m-2=3\\m+1< >2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m=3\\m< >1\end{matrix}\right.\)
=>m=3
f: Để (1) tạo với trục Ox một góc tù thì m-2<0
=>m<2
g: Thay x=0 vào y=5x+6, ta được:
\(y=5\cdot0+6=6\)
Thay x=0 và y=6 vào (1), ta được:
\(0\left(m-2\right)+m+1=6\)
=>m+1=6
=>m=5

\(a,\Leftrightarrow m-1>0\Leftrightarrow m>1\\ b,m=3\Leftrightarrow y=2x+2\\ c,\Leftrightarrow\left\{{}\begin{matrix}m-1\ne2\\2\ne-1\end{matrix}\right.\Leftrightarrow m\ne3\)
y = x + 1 - x 2 + 3 x x 2 + ( m + 1 ) x - m - 2 = ( x + 1 ) 2 - ( x 2 + 3 x ) ( x + 1 + x 2 + 3 x ) ( x - 1 ) ( x + m + 2 ) = - 1 ( x + 1 + x 2 + 3 x ) ( x + m + 2 )
+ Vì bậc tử số < bậc mẫu số nên luôn có một tiệm cận ngang y= 0
+ Vì phương trình x + 1 + x 2 + 3 x = 0 vô nghiệm nên chỉ có duy nhất một tiệm cận đứng nữa đó là đường thẳng x= -m-2.
Vậy với mọi x; đồ thị hàm số đã cho luôn có hai tiệm cận.
Chọn C.