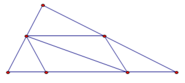
Hình trên có số hình tam giác và tứ giác là:
A. 7 tam giác, 6 tứ giác.
B. 7 tam giác, 5 tứ giác.
C. 7 tam giác, 7 tứ giác.
D. 6 tam giác, 5 tứ giác.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HQ
Hà Quang Minh
Giáo viên
8 tháng 9 2023
Xét \(\Delta ABC\) ta có:
\(\widehat B + \widehat {BAC} + \widehat {BCA} = 180^\circ \) (tính chất tổng ba góc trong tam giác)
Xét \(\Delta DAC\) ta có:
\(\widehat D + \widehat {DAC} + \widehat {DCA} = 180^\circ \)
Ta có:
\(\widehat B + \widehat {BAC} + \widehat {BCA} + \widehat D + \widehat {DAC} + \widehat {DCA} = 180^\circ + 180^\circ \)
\(\widehat B + \widehat D + \left( {\widehat {BAC} + \widehat {DAC}} \right) + \left( {\widehat {BCA} + \widehat {DCA}} \right) = 360^\circ \)
\(\widehat B + \widehat D + \widehat {BAD} + \widehat {BCD} = 360^\circ \)
Vậy tổng các góc của tứ giác \(ABCD\) bằng \(360^\circ \)
CM
3 tháng 6 2017
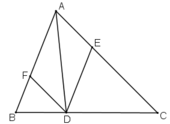
a) Tứ giác AEDF là hình bình hành.
Vì có DE // AF, DF // AE (gt) (theo định nghĩa)
b) Hình bình hành AEDF là hình thoi khi AD là tia phân giác của góc A. Vậy nếu D là giao điểm của tia phân giác góc A với cạnh BC thì AEDF là hình thoi.
c) Nếu ΔABC vuông tại A thì AEDF là hình chữ nhật (vì là hình bình hành có một góc vuông).
d) Nếu ABC vuông tại A và D là giao điểm của tia phân giác của góc A với cạnh BC thì AEDF là hình vuông (vì vừa là hình chữ nhật, vừa là hình thoi).
CM
10 tháng 8 2017
Ta có sơ đồ:
Vậy diện tích hình tứ giác ABED là:
27,2 + 13,6 = 40,8 ( cm 2 )
Diện tích hình tam giác BEC là:
13,6 x 2 = 27,2 ( cm 2 )
Diện tích hình tứ giác ABCD là:
40,8 + 27,2 = 68 ( cm 2 )
Đáp số: 68 cm 2
CM
16 tháng 10 2019
Ta có sơ đồ:
Vậy diện tích hình tứ giác ABED là:
27,2 + 13,6 = 40,8 (cm2)
Diện tích hình tam giác BEC là:
13,6 x 2 = 27,2 (cm2)
Diện tích hình tứ giác ABCD là:
40,8 + 27,2 = 68 (cm2)
Đáp số: 68cm2
Đáp án C