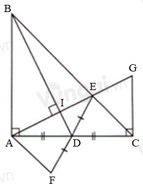
Cho tam giác ABC vuông cân tại A và D là trung điểm AC. Từ A kẻ đường vuông góc với BD, cắt BC tại E. Chọn đáp án đúng
A. AE = 3DE
B. AE = 3 2 DE
C. AE = 2DE
D. AE = DE
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
31 tháng 12 2018
Đúng(0)
Những câu hỏi liên quan
7 tháng 5 2017
Gọi I là giao điềm của AE và BD. Lấy trung điểm của AE là K. Nối K với D.
Xét tam giác AEC: K là trung điểm của AE, D là trung điểm của AC => KD là đường trung bình của tam giác AEC.
=> KD//EC và KD=1/2EC (1) (Tính chất đường trung bình trong tam giác)
Do AE vuông góc với BD => Tam giác ABI vuông tại I. Mà tam giác BAD vuông tại A
=> Tam giác ABI đồng dạng với tam giác BAD. (g.g)
=> BI/AI = AB/AD=2 (Tính chất của 2 tam giác đồng dạng) => BI=2AI (2)
Song lại có: Tam giác AID vuông tại I => Tam giác AID đồng dạng với tam giác BAD.
=> ID/IA=AD/AB=1/2 => AI=2ID (3)
Từ (2) và (3) => BI=2AI=2.2.ID=4ID => BI=4ID => ID/IB=1/4
Do KD//EC (cmt) => KD/BE=DI/IB=1/4 => KD=1/4BE (4)
Từ (1) và (4) => KD=1/2EC=1/4BE => BE=2EC => EC/BE=1/2=DC/AB
Vì tam giác ABC vuông cân tại A => ^B=^C=450 => Tam giác ABE đồng dạng với tam giác DCE (c.g.c)
=> ^E1=^E2.(5)
KD//EC hay KD//BC => ^DKE=^E1 và ^KDE=^E2 (6)
Từ (5) và (6) => ^DKE=^KDE => Tam giác KED cân tại E
=> DE=KE. Mà K là trung điểm của AE => KE=1/2AE =>DE=1/2AE=> AE=2DE (đpcm)
Mình giải theo cách của lớp 8 . Bạn có gì thắc mắc thì cứ hỏi.
--Good Luck--
16 tháng 12 2023
a) Ta có:
- Góc ABD là góc giữa hai phân giác của góc ABC, nên ABD = CBD.
- Góc EBD là góc giữa phân giác của góc ABC và đường thẳng DE, nên EBD = CBD.
Vậy tam giác ABD = tam giác EBD.
b) Ta có:
- Góc ABD = góc EBD (do chứng minh ở câu a).
- Góc ADB = góc EDB (do cùng là góc vuông).
- Vậy tam giác ABD = tam giác EBD (do hai góc bằng nhau và góc giữa hai cạnh bằng nhau).
- Do đó, BD vuông góc với AE.
- Ta có AE cắt BD tại I, vậy I là trung điểm của AE.
c) Ta có:
- Tia Cx vuông góc với tia BD tại H.
- Trên tia đối của tia AB, lấy điểm F sao cho AF = EC.
- Ta cần chứng minh 3 điểm C, H, F thẳng hàng và AE // FC.
- Vì AF = EC và tam giác ABD = tam giác EBD (do chứng minh ở câu a), nên tam giác AFB = tam giác EFC (do hai cạnh bằng nhau và góc giữa hai cạnh bằng nhau).
- Vậy 3 điểm C, H, F thẳng hàng và AE // FC.
16 tháng 12 2023
a: Xét ΔBAD vuông tại A và ΔBED vuông tại E có
BD chung
\(\widehat{ABD}=\widehat{EBD}\)
Do đó: ΔBAD=ΔBED
b: Ta có: ΔBAD=ΔBED
=>BA=BE và DA=DE
Ta có: BA=BE
=>B nằm trên đường trung trực của AE(1)
Ta có: DA=DE
=>D nằm trên đường trung trực của AE(2)
Từ (1) và (2) suy ra BD là đường trung trực của AE
=>BD vuông góc với AE tại trung điểm I của AE
c: Xét ΔBFC có \(\dfrac{BA}{AF}=\dfrac{BE}{EC}\)
nên AE//CF
Ta có: BD\(\perp\)AE
AE//CF
Do đó: BD\(\perp\)CF
mà BD\(\perp\)CH
và CH,CF có điểm chung là C
nên C,H,F thẳng hàng
16 tháng 4 2023
a: Xet ΔBAD vuông tại A và ΔBED vuông tại E có
BD chung
góc ABD=góc EBD
=>ΔBAD=ΔBED
b: ΔBAE cân tại B
mà BM là phân giác
nên BM vuông góc AE tại M và M là trung điểm của AE
10 tháng 5 2023
a: Xét ΔBAD vuông tại A và ΔBED vuông tại E có
BD chung
góc ABD=góc EBD
=>ΔBAD=ΔBED
b: ΔBAD=ΔBED
=>DA=DE
=>ΔDAE cân tại D
=>góc DAE=góc DEA
c: BA=BE
DA=DE
=>BD là trung trực của AE