Trên mặt phẳng tọa độ Oxy, vẽ các điểm A(-2;1);B(-6;1);C(-6;6) và D(-2;6). Tứ giác ABCD là hình gì?
A. Hình vuông
B. Hình chữ nhật
C. Hình bình hành
D. Chưa đủ điều kiện xác định
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
Áp dụng định lý Pitago: $OA=\sqrt{1^2+1^2}=\sqrt{2}$
Vì $B\in Ox$ nên tọa độ của $B$ có dạng $(b,0)$
Vì $B$ thuộc đường tròn tâm $O$ bán kính $OA=\sqrt{2}$ nên $|x_B|=OB=OA=\sqrt{2}$. Vậy $B(\pm \sqrt{2},0)$
$C\in Oy$ nên $C$ có tọa độ $(0,c)$
$C$ thuộc đường tròn đường kính $OA$ nên:
$|y_C|=OC=OA=\sqrt{2}$. Vậy $C(0, \pm \sqrt{2})$

a: 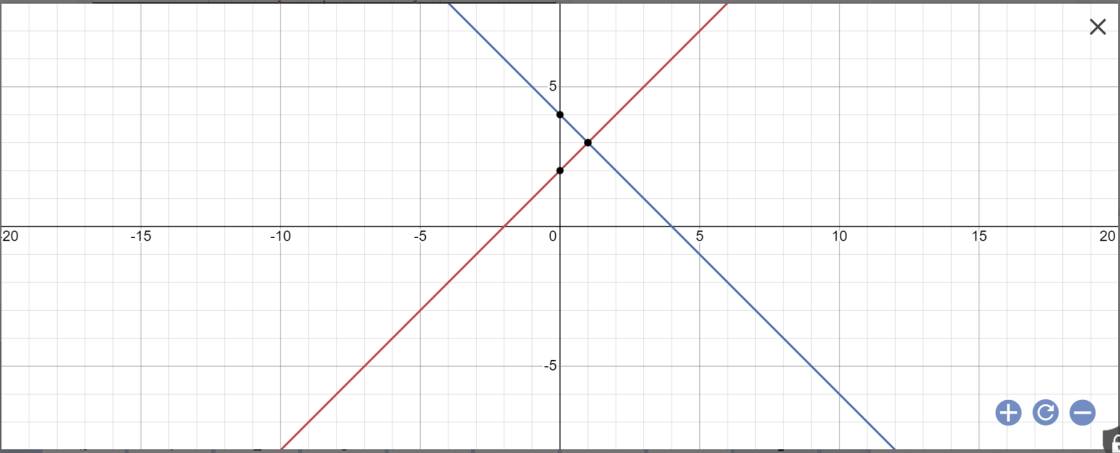
b: Tọa độ giao điểm của (d1) và (d2) là:
\(\left\{{}\begin{matrix}x+2=-x+4\\y=x+2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2x=2\\y=x+2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=1+2=3\end{matrix}\right.\)
Thay x=1 và y=3 vào (d3), ta được:
\(1\cdot m+m=3\)
=>2m=3
=>\(m=\dfrac{3}{2}\)

Hình chữ nhật ABDC có AB=5cm;AC=3cm nên diện tích ABDCABDC bằng 5.3=15( cm 2 )
Đáp án cần chọn là: A

Vẽ các điểm A(3;1);B(-2;1);C(3;4) và D(-2;4) trên cùng mặt phẳng tọa độ
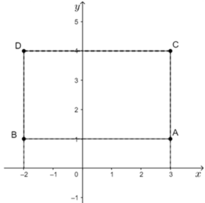
Theo hình vẽ ta thấy ABCD là hình chữ nhật
Đáp án cần chọn là B

\(a,\) Thay \(x=3;y=4\Rightarrow\dfrac{4}{3}\cdot3=4\) (đúng)
Vậy \(A\left(3;4\right)\in y=\dfrac{4}{3}x\)
Vẽ các điểm A(-2;1);B(-6;1);C(-6;6) và D(-2;6) trên cùng mặt phẳng tọa độ
Ta thấy ABCD là hình chữ nhật
Đáp án cần chọn là B