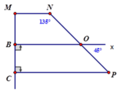
Cho hình vẽ dưới đây. Chứng minh rằng MN // CP và M N ⊥ B C
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
13 tháng 6 2022
a: Xét ΔABC có
M là trung điểm của AB
N là trung điểm của AC
DO đó: MNlà đường trug bình
=>MN//BC và MN=1/2BC
=>MP=BC
Xét tứ giác BMPC có
MP//BC
MP=BC
Do đó: BMPC là hình bìnhhành
Suy ra: MB=PC
b: Xét ΔBMC và ΔPCM có
BM=PC
MC chung
BC=PM
Do đó: ΔBMC=ΔPCM
*Ta có B O N ^ = P O x ^ = 45 ° (đối đỉnh) suy ra B O N ^ + O N M ^ = 135 ° + 45 ° = 180 ° mà 2 góc này ở vị trí trong cùng phía nên MN // BO.
* B C ⊥ B O B C ⊥ C P ⇒ B O / / C P ( từ vuông góc đến song song) mà B O / / M N = > ⇒ B O / / M N / / C P (ba đường thẳng song song)
* B C ⊥ C P C P / / M N ⇒ M N ⊥ B C ( từ song song đến vuông góc)