Cho (O) đường kính ab và c thuộc (o) sao cho ca>cb. Từ C vẽ d là tiếp tuyến của đường tròn (o). Gọi D, E lần lượt là hình chiếu vuông góc của A, B lên đường thẳng d a) cmr: C là trung điểm DE b) cmr: Tam giác ACB vuông c) cmr: BC là phân giác của góc ABE d) cmr: AB là tiếp tuyến của đường tròn đường kính DE
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

hình ông tự vẽ nha
kẻ OH vuông góc với CD
Kẻ OK là trung tuyến của tam giác CMD
xét tam giác CMD vuông tại M có
MK=CK = 1/2 CD (MK là tiếp tuyến )
=> CKM là tam giác cân, cân tại K
=> góc MKC = góc KMC
AC vuông góc với AB
BD vuông góc với AB
=> AC // BD
=>ACBD là hình thang
AM = MB
CK=KD
=>MK là đường trung bình
=> MK // CA
=> góc ACM = góc KMC
mà góc KMC = góc KCM (cmt)
=> góc ACM = góc KCM
=> góc HMC= góc CMA (cùng phụ 2 góc đó)
xét tam giác MAC và tam giác MHC có:
góc CAM = góc CHM = 90 độ
góc ACM= góc HCM ( cmt)
=> góc HMC= góc CMA
=> tam giác MAC = tam giác MHC
=> HM = AM mà HM vuông CD => ĐPCM
bài có ít sai sót ông xem thử nha

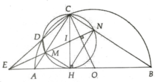
a, Tứ giác CMHN là hình chữ nhật
b, Ta có
O
C
A
^
=
O
A
C
^
C B A ^ = A C H ^ ; A C H ^ = C M N ^
=> O C A ^ + C M N ^ = 90 0
Vậy OC ⊥ MN
c, Ta có ∆IOC có E là trực tâm suy ra IN đi qua M và E (đpcm)
d, Ta có E M A ^ = C M N ^ ; C M N ^ = C B A ^ => ∆EMA:∆ENB
Tương tự ∆EMH:∆EHN => EM.EN = E H 2 ngoài ra , ∆EHC vuông tại H có HD là đường cao
=> E H 2 = ED.EC. Từ đó ta có đpcm

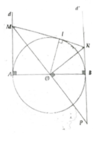
a, ∆MAO = ∆PBO => MO = OP => ∆MNP cân
Vì đường cao NO đồng thời là đường trung tuyến
b, 1 O I 2 - 1 O M 2 + 1 O N 2
= 1 O P 2 + 1 O N 2 = 1 O B 2 => OI = R
=> MN là tiếp tuyến của (O)
c, AM.BN = MI.IN = O I 2 = R 2
d, S A M N B = M N . A B 2
=> S A M N B min
<=> M N m i n <=> AM = R

1: góc MAI+góc MEI=180 độ
=>MAIE nội tiếp
2: góc IEN+góc IBN=180 độ
=>IENB nội tiếp
MAIE nội tiếp
=>góc AMI=góc AEI
IENB nội tiếp
=>góc BIN=góc BEN
góc BEN+góc IEB=90 độ
góc AEI+góc BEI=90 độ
=>góc BEN=góc AEI
=>góc AMI=góc BIN

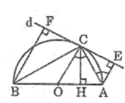
Tam giác ABC nội tiếp trong đường tròn (O) có AB là đường kính nên góc (ACB) = 90 °
Tam giác ABC vuông tại C có CH ⊥ AB
Theo hệ thức liên hệ giữa đường cao và hình chiếu, ta có:
C H 2 = HA.HB (3)
Xét hai tam giác ACH và ACE, ta có:
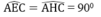
CH = CE (tính chất đường phân giác)
AC chung
Suy ra : ∆ ACH = ∆ ACE (cạnh huyền, cạnh góc vuông)
Suy ra: AH = AE (4)
Xét hai tam giác BCH và BCF, ta có:
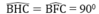
CH = CF (= CE)
BC chung
Suy ra: ∆ BCH = ∆ BCF (cạnh huyền, cạnh góc vuông)
Suy ra: BH = BF (5)
Từ (3), (4) và (5) suy ra: C H 2 = AE.BF

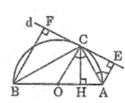
Ta có: OC ⊥ d (tính chất tiếp tuyến)
AE ⊥ d (gt)
BF ⊥ d (gt)
Suy ra : OC // AE // BF
Mà OA = OB (= R)
Suy ra: CE = CF (tính chất đường thẳng song song cách đều)
b: Xét (O) có
ΔACB nội tiếp đường tròn
AB là đường kính
Do đó: ΔACB vuông tại C