i) Thực hiện các phép tính:
b ) x 3 2 y x - 2 y : x 2 2 x 2 y - 8 y 3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
30 tháng 7 2018
Đúng(0)
Những câu hỏi liên quan
22 tháng 7 2023
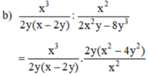
`a, (4x^3y^2 - 8x^2y + 10xy) : 2xy`
`= 2x^2y - 4x + 5`.
`b, 7x^4y^2 - 2x^2y^2 - 5x^3y^4 : 3x^2y`
`= 7/3 x^2y - 3/2y - 5/3xy^3`
H9
HT.Phong (9A5)
CTVHS
23 tháng 7 2023
a) \(18x^4y^3:12\left(-x\right)^3y\)
\(=\left(18:-12\right)\left(x^4:x^3\right)\left(y^3:y\right)\)
\(=-\dfrac{3}{2}xy^2\)
b) \(x^2y^2-2xy^3:\dfrac{1}{2}xy^2\)
\(=\dfrac{xy^2\left(x-2y\right)}{\dfrac{1}{2}xy^2}\)
\(=\dfrac{x-2y}{\dfrac{1}{2}}\)
\(=2x-4y\)
H9
HT.Phong (9A5)
CTVHS
23 tháng 7 2023
a) \(x^2y\left(5xy-2x^2y-y^2\right)\)
\(=5x^3y^2-2x^4y^2-x^2y^3\)
b) \(\left(x-2y\right)\left(2x^3+4xy\right)\)
\(=2x^4+4x^2y-4x^3y-8xy^2\)
H
22 tháng 7 2023
\(a,\dfrac{x}{x+3}+\dfrac{2-x}{x+3}\\ =\dfrac{x+2-x}{x+3}\\ =\dfrac{2}{x+3}\\b,\dfrac{x^2y}{x-y}-\dfrac{xy^2}{x-y}\\ =\dfrac{x^2y-xy^2}{x-y}\\ =\dfrac{xy\left(x-y\right)}{x-y}\\ =xy\\ c,\dfrac{2x}{2x-y}+\dfrac{y}{y-2x}\\=\dfrac{2x}{2x-y}-\dfrac{y}{2x-y}\\ =\dfrac{2x-y}{2x-y}\\ =1 \)
22 tháng 7 2023
`a, x/(x+3) + (2-x)/(x+3) = (x+2-x)/(x+3) = 2/(x+3)`
`b, (x^2y)/(x-y) - (xy^2)/(x-y) = (x^2y-xy^2)/(x-y) = (xy(x-y))/(x-y)= xy`
`c, (2x)/(2x-y) - (y)/(2x-y)`
`= (2x-y)/(2x-y) = 1`
2 tháng 12 2023
Bài 2:
1: \(A=\left(x+2\right)\left(x^2-2x+4\right)+2\left(x+1\right)\left(1-x\right)\)
\(=\left(x+2\right)\left(x^2-x\cdot2+2^2\right)-2\left(x+1\right)\left(x-1\right)\)
\(=x^3+2^3-2\left(x^2-1\right)\)
\(=x^3+8-2x^2+2=x^3-2x^2+10\)
\(B=\left(2x-y\right)^2-2\left(4x^2-y^2\right)+\left(2x+y\right)^2+4\left(y+2\right)\)
\(=\left(2x-y\right)^2-2\cdot\left(2x-y\right)\left(2x+y\right)+\left(2x+y\right)^2+4\left(y+2\right)\)
\(=\left(2x-y-2x-y\right)^2+4\left(y+2\right)\)
\(=\left(-2y\right)^2+4\left(y+2\right)\)
\(=4y^2+4y+8\)
2: Khi x=2 thì \(A=2^3-2\cdot2^2+10=8-8+10=10\)
3: \(B=4y^2+4y+8\)
\(=4y^2+4y+1+7\)
\(=\left(2y+1\right)^2+7>=7>0\forall y\)
=>B luôn dương với mọi y
Bài 1:
5: \(x^2\left(x-y+1\right)+\left(x^2-1\right)\left(x+y\right)\)
\(=x^3-x^2y+x^2+x^3+x^2y-x-y\)
\(=2x^3-x+x^2-y\)
6: \(\left(3x-5\right)\left(2x+11\right)-6\left(x+7\right)^2\)
\(=6x^2+33x-10x-55-6\left(x^2+14x+49\right)\)
\(=6x^2+23x-55-6x^2-84x-294\)
=-61x-349
29 tháng 6 2021
`a)A=x(x+y)-x(y-x)`
`=x^2+xy-xy+x^2`
`=2x^2`
Thay `x=-3`
`=>A=2.9=18`
`b)B=4x(2x+y)+2y(2x+y)-y(y+2x)`
`=8x^2+4xy+4xy+2y^2-y^2-2xy`
`=8x^2+y^2+6xy`
Thay `x=1/2,y=-3/4`
`=>B=8*1/4+9/16-9/4`
`=2+9/16-9/4`
`=9/16-1/4=5/16`
MH
18 tháng 2 2022
\(\left(\dfrac{x}{x+1}+\dfrac{x-1}{x}\right):\left(\dfrac{x}{x+1}-\dfrac{x-1}{x}\right)\) \(\left(đk:x\ne0;-1\right)\)
\(=\dfrac{x^2+\left(x-1\right)\left(x+1\right)}{x\left(x+1\right)}:\left(\dfrac{x^2-\left(x-1\right)\left(x+1\right)}{x\left(x+1\right)}\right)\)
\(=\dfrac{x^2+x^2-1}{x\left(x+1\right)}.\dfrac{x\left(x+1\right)}{x^2-x^2+1}\)
\(=\dfrac{\left(2x^2-1\right)x\left(x+1\right)}{x\left(x+1\right)}=2x^2-1\)
10 tháng 12 2020
a) \(\left(x^5+4x^3-6x^2\right):4x^2\)
\(=\left(x^5:4x^2\right)+\left(4x^3:4x^2\right)+\left(-6x^2:4x^2\right)\)
\(=\dfrac{1}{4}x^3+x-\dfrac{3}{2}\)
b)
Vậy \(\left(x^3+x^2-12\right):\left(x-2\right)=x^2+3x+6\)
c) (-2x5 : 2x2) + (3x2 : 2x2) + (-4x^3 : 2x^2)
= \(-x^3+\dfrac{3}{2}-2x\)
d) \(\left(x^3-64\right):\left(x^2+4x+16\right)\)
\(=\left(x-4\right)\left(x^2+4x+16\right):\left(x^2+4x+16\right)\)
\(=x-4\)
(dùng hẳng đẳng thức thứ 7)
Bài 2 :
a) 3x(x - 2) - 5x(1 - x) - 8(x2 - 3)
= 3x2 - 6x - 5x + 5x2 - 8x2 + 24
= (3x2 + 5x2 - 8x2) + (-6x - 5x) + 24
= -11x + 24
b) (x - y)(x2 + xy + y2) + 2y3
= x3 - y3 + 2y3
= x3 + y3
c) (x - y)2 + (x + y)2 - 2(x - y)(x + y)
= (x - y)2 - 2(x - y)(x + y) + (x + y)2
= [(x - y) + x + y)2 = [x - y + x + y] = (2x)2 = 4x2
18 tháng 10 2021
Bài 1 :
a]= \(\frac{1}{4}\)x3 + x - \(\frac{3}{2}\).
b] => [x3 + x2 -12 ] = [ x2 +3 ][x-2] + [-6]
c]= -x3 -2x +\(\frac{3}{2}\).
d] = [ x3 - 64 ] = [ x2 + 4x + 16][ x- 4].
30 tháng 5 2022
a: \(=x^2-xy+xy+y^2=x^2+y^2=100\)
b \(=x^3-xy-x^3-x^2y+x^2y-xy=-2xy=-2\cdot\dfrac{1}{2}\cdot\left(-100\right)=-1\cdot\left(-100\right)=100\)
TC
30 tháng 5 2022
a)` x(x - y) + y(x + y) `
`=x^2-xy+xy+y^2`
`=x^2+y^2`(1)
thay x= -6 ; y= 8 vào 1 ta đc
\(\left(-6\right)^2+8^2=36+64=100\)
b)`) x(x^2 - y) - x^2 (x + y) + y (x^2 - x) `
`=x^3-xy-x^3-xy+yx^2-xy`
`=\(-3xy+yx^2\)(2)
thay `x= 1/2 và y = -100` ta đc
\(-\dfrac{3.1}{2}.\left(-100\right)+\dfrac{\left(-100\right).1}{2}=150-50=100\)
23 tháng 7 2023
a: \(=\dfrac{2x^2-1-x^2-3}{x-2}=\dfrac{x^2-4}{x-2}=x+2\)
b: \(=\dfrac{x\left(x-y\right)+y\left(x+y\right)}{\left(x+y\right)\left(x-y\right)}\)
\(=\dfrac{x^2-xy+xy+y^2}{x^2-y^2}=\dfrac{x^2+y^2}{x^2-y^2}\)
c: \(=\dfrac{x+1-2}{\left(x-1\right)\left(x+1\right)}=\dfrac{\left(x-1\right)}{\left(x-1\right)\left(x+1\right)}=\dfrac{1}{x+1}\)
d: \(=\dfrac{\left(x+2\right)\cdot y-x\left(y-2\right)}{xy\left(x+y\right)}\)
\(=\dfrac{2y+2x}{xy\left(x+y\right)}=\dfrac{2}{xy}\)
e: \(=\dfrac{1}{x\left(2x-3\right)}-\dfrac{1}{\left(2x-3\right)\left(2x+3\right)}\)
\(=\dfrac{2x+3-x}{x\left(2x-3\right)\left(2x+3\right)}=\dfrac{x+3}{x\left(2x-3\right)\left(2x+3\right)}\)
g: \(=\dfrac{-2x+x+3-x+3}{\left(x-3\right)\left(x+3\right)}=\dfrac{-2x+6}{\left(x-3\right)\left(x+3\right)}=\dfrac{-2}{x+3}\)