Cho đường tròn (O) bán kính OA và đường tròn (O') đường kính OA. Vị trí tương đối của hai đường tròn là:
A. Nằm ngoài nhau
B. Cắt nhau
C. Tiếp xúc ngoài
D. Tiếp xúc trong
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Gọi E là trung điểm của OA
=>E là tâm đường tròn đường kính OA
Xét (E) có
ΔOBA nội tiếp
OA là đường kính
Do đó: ΔOBA vuông tại B
=>AB vuông góc OB tại B
=>AB là tiếp tuyến của (O)
Xét (O) có
ΔOCA nội tiếp
OA là đường kính
Do đó: ΔOCA vuông tại C
=>AC vuông góc với CO tại C
=>AC là tiếp tuyến của (O)
b: Xét (O) có
ΔBCK nội tiếp
BK là đường kính
Do đó: ΔBCK vuông tại C
=>BC vuông góc CK tại C
Xét (E) có
ΔBCI nội tiếp
BI là đường kính
Do đó: ΔBCI vuông tại C
=>BC vuông góc CI tại C
\(\widehat{KCI}=\widehat{KCB}+\widehat{ICB}\)
\(=90^0+90^0\)
\(=180^0\)
=>K,C,I thẳng hàng
Xét (B;BC) có
BC là bán kính
KI vuông góc với BC tại C
Do đó: KI là tiếp tuyến của (B;BC)

BD//CE
Ax là tiếp tuyến
=>Ax//BD//CE
=>Tâm đường tròn ngoại tiếp ΔOIO' nằm trên Ax
=>BC là tiếp tuyến của đường tròn ngoại tiếp ΔOIO'

Đáp án D
Hai đường tròn có một điểm chung là A nên hai đường tròn tiếp xúc nhau.
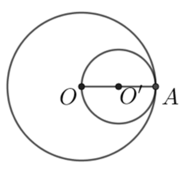
Chọn đáp án D
Vì hai đường tròn có một điểm chung là A và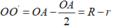 nên hai đường tròn tiếp xúc trong
nên hai đường tròn tiếp xúc trong