Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp án D
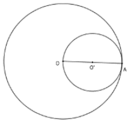
Vì hai đường tròn có một điểm chung là A và 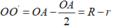 nên hai đường tròn tiếp xúc trong
nên hai đường tròn tiếp xúc trong

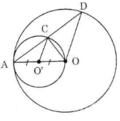
a) Gọi O’ là tâm của đường tròn đường kính OA.
Gọi R và r lần lượt là bán kính đường tròn tâm O và tâm O’.

Suy ra, hai đường tròn đã cho tiếp xúc trong với nhau.
b) +) Xét đường tròn (O’) có A, O, C là ba điểm cùng thuộc đường tròn và OA là đường kính nên tam giác AOC vuông tại C.
⇒ OC ⊥ AD
+) Xét đường tròn tâm (O) có A, D là hai điểm thuộc đường tròn nên OA = OD
⇒ ΔAOD cân tại O mà OC ⊥ AD
⇒ OC là đường trung tuyến của ΔAOD
⇒ C là trung điểm của AD
⇒ AC = CD

Hướng dẫn giải:

a) Gọi O' là tâm của đường tròn đường kính OA thì O'A=O'O.
Ta có OO'=OA-O'A hay d=R-r nên đường tròn (O) và đường tròn (O') tiếp xúc trong.
b) Tam giác CAO có cạnh OA là đường kính của đường tròn ngoại tiếp nên ΔCAO vuông tại C
⇒OC⊥AD
⇒CA=CD (đường kính vuông góc với một dây).

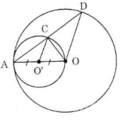
Gọi O’ là tâm của đường tròn đường kính OA.
Gọi R và r lần lượt là bán kính đường tròn tâm O và tâm O’.

Suy ra, hai đường tròn đã cho tiếp xúc trong với nhau.

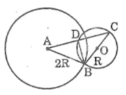
Ta có: R < OA < 3R ⇔ 2R – R < OA < 2R + R
Suy ra hai đường tròn (O ; R) và (A ; 2R) cắt nhau

a: Gọi E là trung điểm của OA
=>E là tâm đường tròn đường kính OA
Xét (E) có
ΔOBA nội tiếp
OA là đường kính
Do đó: ΔOBA vuông tại B
=>AB vuông góc OB tại B
=>AB là tiếp tuyến của (O)
Xét (O) có
ΔOCA nội tiếp
OA là đường kính
Do đó: ΔOCA vuông tại C
=>AC vuông góc với CO tại C
=>AC là tiếp tuyến của (O)
b: Xét (O) có
ΔBCK nội tiếp
BK là đường kính
Do đó: ΔBCK vuông tại C
=>BC vuông góc CK tại C
Xét (E) có
ΔBCI nội tiếp
BI là đường kính
Do đó: ΔBCI vuông tại C
=>BC vuông góc CI tại C
\(\widehat{KCI}=\widehat{KCB}+\widehat{ICB}\)
\(=90^0+90^0\)
\(=180^0\)
=>K,C,I thẳng hàng
Xét (B;BC) có
BC là bán kính
KI vuông góc với BC tại C
Do đó: KI là tiếp tuyến của (B;BC)



Đáp án D
Hai đường tròn có một điểm chung là A nên hai đường tròn tiếp xúc nhau.