Một đa giác có số đường chéo bằng số cạnh của đa giác thì đa giác có số cạnh là?
A. 5.
B. 6.
C. 4.
D. 7.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Số đường chéo của đa giác n cạnh là (n( n - 3 ))/2. ( n ∈ N, n ≥ 3 )
Theo giả thiết ta có (n( n - 3 ))/2 = n ⇔ n( n - 3 ) = 2n ⇔ n 2 - 3 n - 2 n = 0
⇔
n
2
-
5
n
=
0
⇔
n
(
n
-
5
)
=
0
⇔ 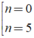
So sánh điều kiện ta có n = 5 thỏa mãn.
Chọn A

Số đường chéo của đa giác n cạnh là (n( n - 3 ))/2.
Khi đó số đường chéo của đa giác 7 cạnh là (7( 7 - 3 ))/2 = 14 (đường chéo)
Chọn đáp án C.

Số đường chéo của đa giác n cạnh là (n( n - 3 ))/2.
Khi đó số đường chéo của đa giác 7 cạnh là (7( 7 - 3 ))/2 = 14 (đường chéo)
Chọn đáp án C.

Cứ hai đỉnh của đa giác ![]() đỉnh tạo thành một đoạn thẳng (bao gồm cả cạnh đa giác và đường chéo).
đỉnh tạo thành một đoạn thẳng (bao gồm cả cạnh đa giác và đường chéo).
Khi đó số đường chéo là: 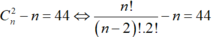
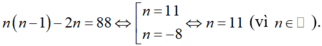
Chọn A.

Cứ hai đỉnh của đa giác n n ∈ ℕ , n ≥ 3 đỉnh tạo thành một đoạn thẳng (bao gồm cả cạnh đa giác và đường chéo).Do đó,đa giác có tất cả C n 2 đường chéo và cạnh
Đa giác n thì có n cạnh nên số đường chéo của đa giác là:
C n 2 − n = 44 ⇔ n ! n − 2 ! .2 ! − n = 44 ⇒ n ( n − 1 ) 2 − n = 44
⇔ n n − 1 − 2 n = 88 ⇔ n 2 − 3 n − 88 = 0 ⇔ n = 11 n = − 8 ⇔ n = 11 (vì n ∈ ℕ ).
Chọn đáp án A.
a) Tính số đường chéo của đa giác có 24 cạnh
b) Tính số cạnh của đa giác biết đường chéo là 170 đường

a) \(\frac{\left(24-3\right).24}{2}=252\)đường chéo
b) \(\left(n-3\right).n=340\)
\(n^2-3n=340\)
\(n^2-3n-340=0\)
\(n^2-20n+17n-340=0\)
\(n\left(n-20\right)+17\left(n-20\right)\)
\(\left(n+17\right)\left(n-20\right)=0\)
\(\Leftrightarrow\)\(\orbr{\begin{cases}n+17=0\\n-20=0\end{cases}}\)\(\Leftrightarrow\)\(\orbr{\begin{cases}n=-17\\n=20\end{cases}}\)
n = -17 ( loại )
n = 20 ( nhận )
Vậy n = 20 hay số cạnh của đa giác là 20
1 Đa giác có n cạnh có :
- Số đường chéo từ 1 đỉnh là : (n - 3)
- Số đỉnh là n
Do 1 đường chéo nối 2 đỉnh
=> 1 Đa giác có n cạnh có n(n - 3)/2 đường chéo
biết tổng số đường chéo là 170
=> n(n - 3)/2 = 170
=> n² - 3n - 340 = 0
∆ = (-3)² - 4.(-340) = 1369
=> √∆ = 37
=> n = ... (tự giải)