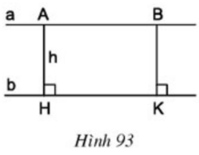
Cho hai đường thẳng song song a và b (h.93).
Gọi A và B là hai điểm bất kì thuộc đường thẳng a, AH và BK là các đường vuông góc kẻ từ A và B đến đường thẳng b. Gọi độ dài AH là h. Tính độ dài BK theo h.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔABC có AC>AB
mà HC,HB lần lượt là hình chiếu của AC,AB trên BC
nên HC>HB
b: Xét ΔDBC có HB<HC
mà HB,HC lần lượt là hình chiếu của DB,DC trên BC
nên DB<DC

a) Ta có:
\(\left. \begin{array}{l}AH \bot \left( P \right)\\BK \bot \left( P \right)\end{array} \right\} \Rightarrow AH\parallel BK\)
Mà \(AB\parallel HK\)
\( \Rightarrow ABKH\) là hình bình hành có \(AH \bot \left( P \right) \Rightarrow AH \bot HK \Rightarrow \widehat {AHK} = {90^ \circ }\)
Vậy \(ABKH\) là hình chữ nhật.
Vậy \(AH = BK\).
b) Ta có:
\(\left. \begin{array}{l}AH \bot \left( Q \right)\\BK \bot \left( Q \right)\end{array} \right\} \Rightarrow AH\parallel BK\)
Mà \(AB\parallel HK\)
\( \Rightarrow ABKH\) là hình bình hành có \(AH \bot \left( Q \right) \Rightarrow AH \bot HK \Rightarrow \widehat {AHK} = {90^ \circ }\)
Vậy \(ABKH\) là hình chữ nhật.
Vậy \(AH = BK\).

\(\left. \begin{array}{l}\Delta \bot \left( P \right)\\a \subset \left( P \right)\end{array} \right\} \Rightarrow \Delta \bot a,a//b \Rightarrow \Delta \bot b \Rightarrow \left( {\Delta ,b} \right) = {90^0}\)
\(\Delta \bot a \Rightarrow \left( {\Delta ,a} \right) = {90^0}\)
\( \Rightarrow \) (\(\Delta \), b) = (\(\Delta \), a) mà b là đường thẳng bất kì thuộc (Q)
\( \Rightarrow \) \(\Delta \bot \left( Q \right)\)

a. xét tam giác vuông AHB và tam giác vuông AHC, có:
AB = AC ( ABC cân )
góc B = góc C ( ABC cân )
Vậy tam giác vuông AHB = tam giác vuông AHC ( ch.gn )
b. ta có: trong tam giác cân ABC đường cao cũng là đường trung tuyến
=> BH = BC :2 = 10 : 2 =5 cm
Áp dụng định lý pitago vào tam giác vuông ABH
\(AB^2=AH^2+BH^2\)
\(\Rightarrow AH=\sqrt{AB^2-BH^2}=\sqrt{13^2-5^2}=\sqrt{144}=12cm\)

a) Xét ΔABC có
BE là đường cao ứng với cạnh AC(gt)
CF là đường cao ứng với cạnh AB(gt)
BE cắt CF tại H(gt)
Do đó: H là trực tâm của ΔABC(Tính chất ba đường cao của tam giác)
Suy ra: AH⊥BC
b) Xét tứ giác BHCK có
HC//BK(gt)
BH//CK(gt)
Do đó: BHCK là hình bình hành(Dấu hiệu nhận biết hình bình hành)
Suy ra: Hai đường chéo HK và BC cắt nhau tại trung điểm của mỗi đường(Định lí hình bình hành)
mà M là trung điểm của BC(gt)
nên M là trung điểm của HK
hay H,M,K thẳng hàng(đpcm)
AH // BK (cùng ⊥ b) và AB // HK ⇒ tứ giác ABKH là hình bình hành
⇒ AH = BK = h